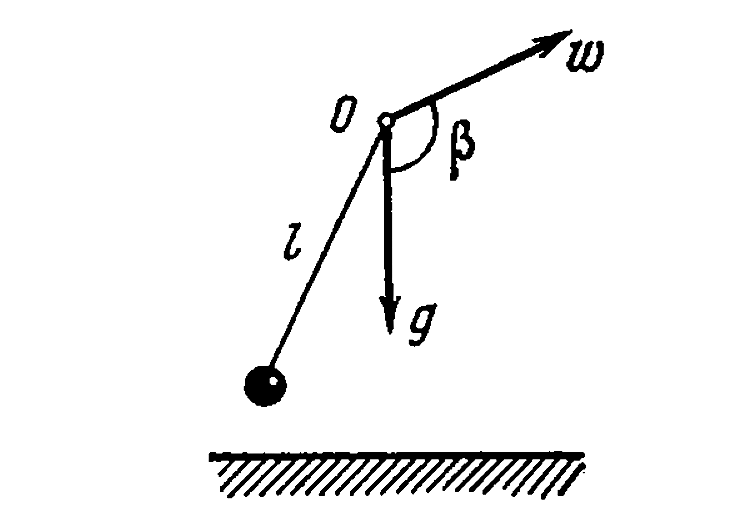Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the period of small oscillations of a mathematical pendulum of le...
Text Solution
|
- Find the period of oscillation of a pendulum of length l if its point ...
Text Solution
|
- A physical pendulum is positioned so that its centre of gravity is abo...
Text Solution
|
- A small ball of mass m suspended from the celling at a point O by a th...
Text Solution
|
- Find the period of small oscillations of a mathematical pendulum of le...
Text Solution
|
- A coical pendulum consists of a string of length L whose upper end is ...
Text Solution
|
- A simple pendulum suspended from the ceilling of a stationary trolley ...
Text Solution
|
- If we have 6% W//W urea solution with density 1.060g//mL , then calcul...
Text Solution
|
- The period of a conical pendulum in terms of its length (l) , semivert...
Text Solution
|