Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS
PRADEEP|Exercise Advanced Problems|20 VideosKINEMATICS
PRADEEP|Exercise NCRT Exercises|22 VideosKINEMATICS
PRADEEP|Exercise 5 Long answer (NCERT)|4 VideosGRAVIATION
PRADEEP|Exercise Assertion-Reason Type Questions|19 VideosLAWS OF MOTION
PRADEEP|Exercise Assertion- Reason Type Questions|17 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-KINEMATICS-6 Long answer (NCERT)
- A hill is 500 m hight. Supplies are to be across the hill using a can...
Text Solution
|
- A gun can fire shells with maximum speed v(0) and the maximum horizont...
Text Solution
|
- A particle is projected in aer an angle beta to a surface which itsel...
Text Solution
|
- A particle falling vertically from a height hits a plane surface incli...
Text Solution
|
- A girl riding a bicycle with a speed of 5 m//s to wards Noth directio...
Text Solution
|
- A river is flowing due east with a speed 3 m//s (Fig. 2 (EP) .31 ). ...
Text Solution
|
- A cricket fielder can throw the cricket ball with a speed v0. If he t...
Text Solution
|
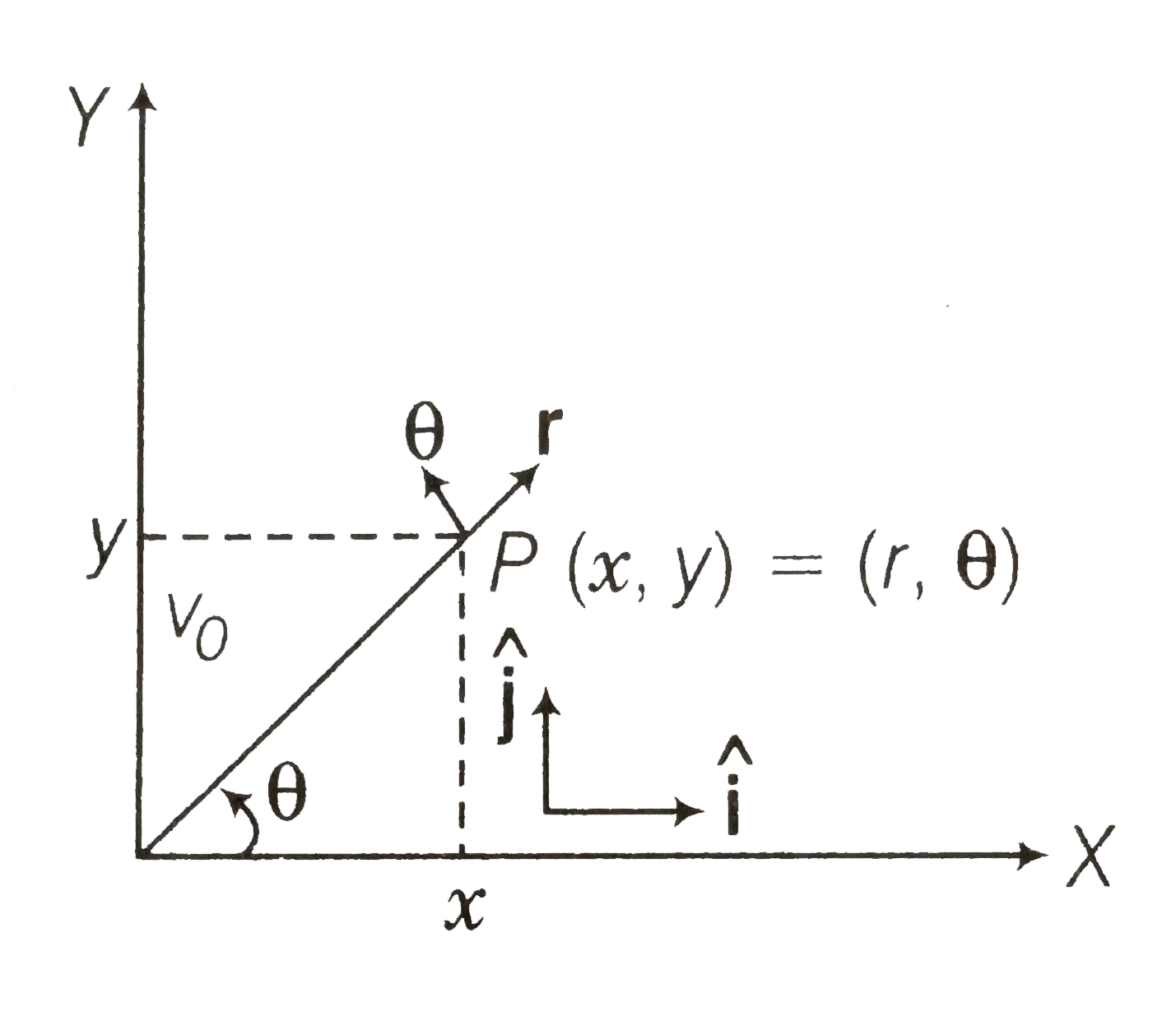
- Motion in two dimensions, in a plane can be studied by expressing posi...
Text Solution
|
- A man wants to reach from A to the opposite corner of the square C. T...
Text Solution
|