Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS
PRADEEP|Exercise Motion|25 VideosKINEMATICS
PRADEEP|Exercise Higher order thinking skills|14 VideosKINEMATICS
PRADEEP|Exercise NCRT Exercises|22 VideosGRAVIATION
PRADEEP|Exercise Assertion-Reason Type Questions|19 VideosLAWS OF MOTION
PRADEEP|Exercise Assertion- Reason Type Questions|17 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-KINEMATICS-Additional Exercises
- A three wheeler starts from rest, accelrates uniformly with 1 ms^(-2)...
Text Solution
|
- A boy standing on a stationary lift ( open from above ) thrown a ball ...
Text Solution
|
- A long belt is moving horizontally with a speed of 5 km h^(-1). A chil...
Text Solution
|
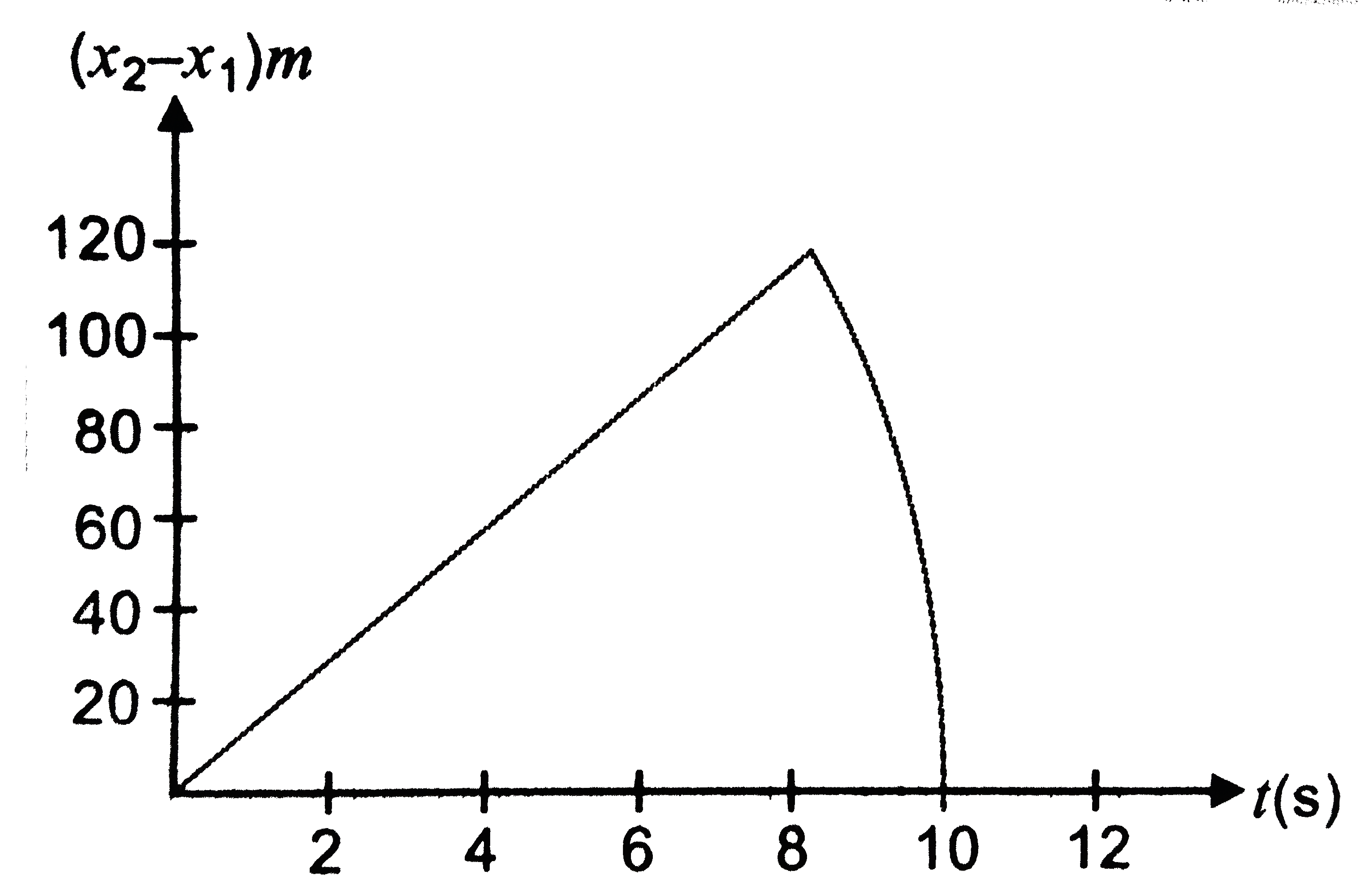
- Two stones are thrown up simultaneously from the edge of a cliff 200 ...
Text Solution
|
- The speed -time graph of a particle moving along a fixed direction id ...
Text Solution
|
- The velocity-time graph of a particle in one-dimensional motion is sho...
Text Solution
|
- A vector has magnitude and dirction 9i) Does it have a olocition in th...
Text Solution
|
- A vector has both magnitude and direction. Does that mean anything tha...
Text Solution
|
- Can you associate vectors with (a) the length of a wire bent into a lo...
Text Solution
|
- A bullet fired at an angle of 30^@ with the horizontal hits the ground...
Text Solution
|
- A fightre plane flying horizontally at an altitude oa 1.5 km with spe...
Text Solution
|
- A cylclist is riding with a speed of 27 km h^-1. As he approaches a ci...
Text Solution
|
- (a) Show that for a projectile the angle between the velocity and the ...
Text Solution
|
 .
.