Text Solution
Verified by Experts
Recommended Questions
- A particle of mass m rests on a horizontal floor with which it has a c...
Text Solution
|
- A particle of mass m rests on a horizontal floor with which it has a c...
Text Solution
|
- A block of mass m rests on a horizontal floor for which coefficient of...
Text Solution
|
- A homogenous block of mass m, width b and height h is resting on a rou...
Text Solution
|
- A blocky of mass m rests on a horizotal floor with which it has a coef...
Text Solution
|
- m द्रव्यमान का एक पिंड एक खुरदरे आनत तल पर जोकि क्षैतिज से theta कोण ब...
Text Solution
|
- A block of mass m is lying on horizontal surface of coefficient of fri...
Text Solution
|
- An inclined plane is inclined at an angle theta with the horizontal. A...
Text Solution
|
- m द्रव्यमान का एक ब्लॉक ऐसे क्षैतिज फर्श पर रखा है जिसके साथ ब्लॉक का ...
Text Solution
|
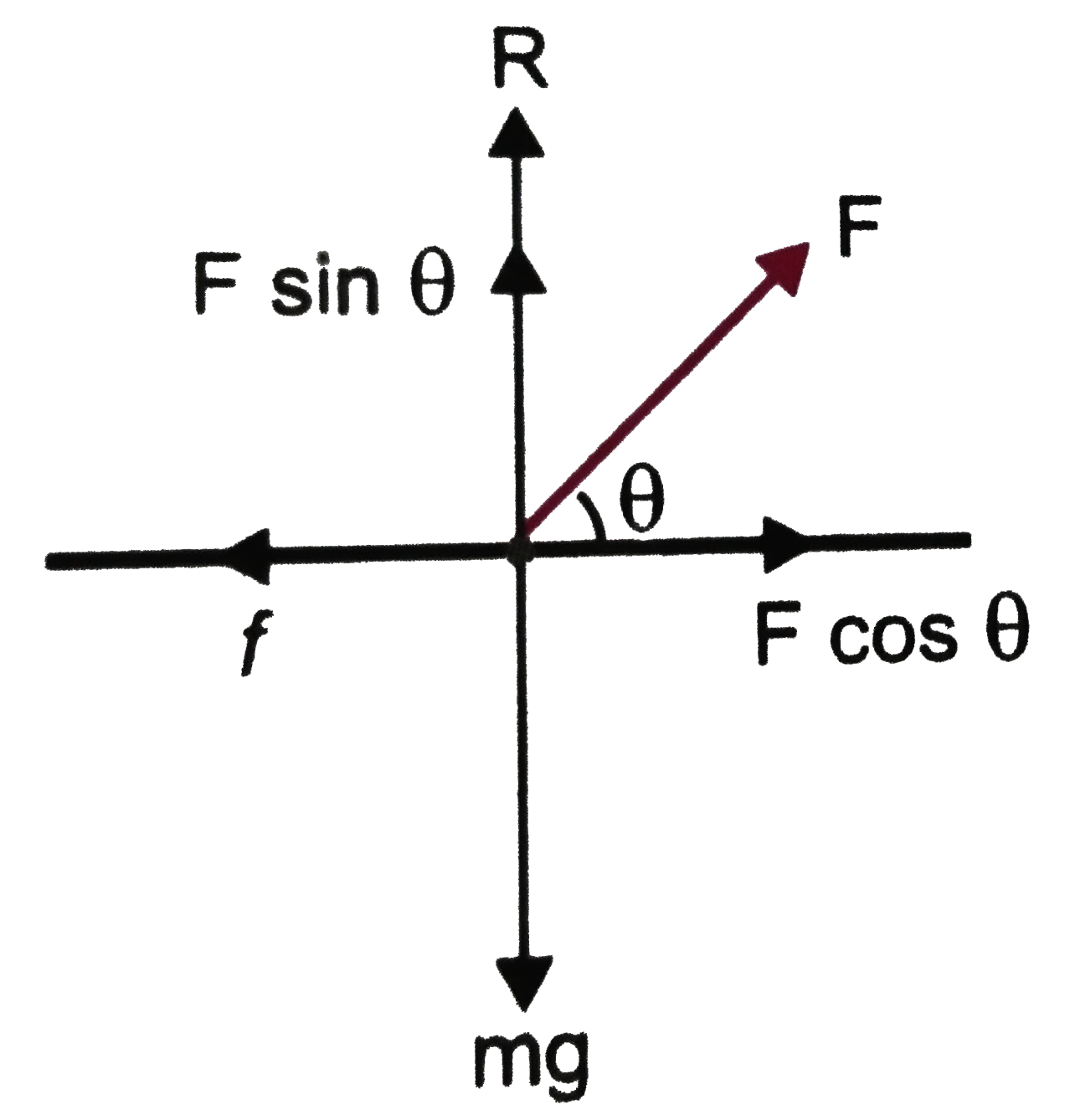
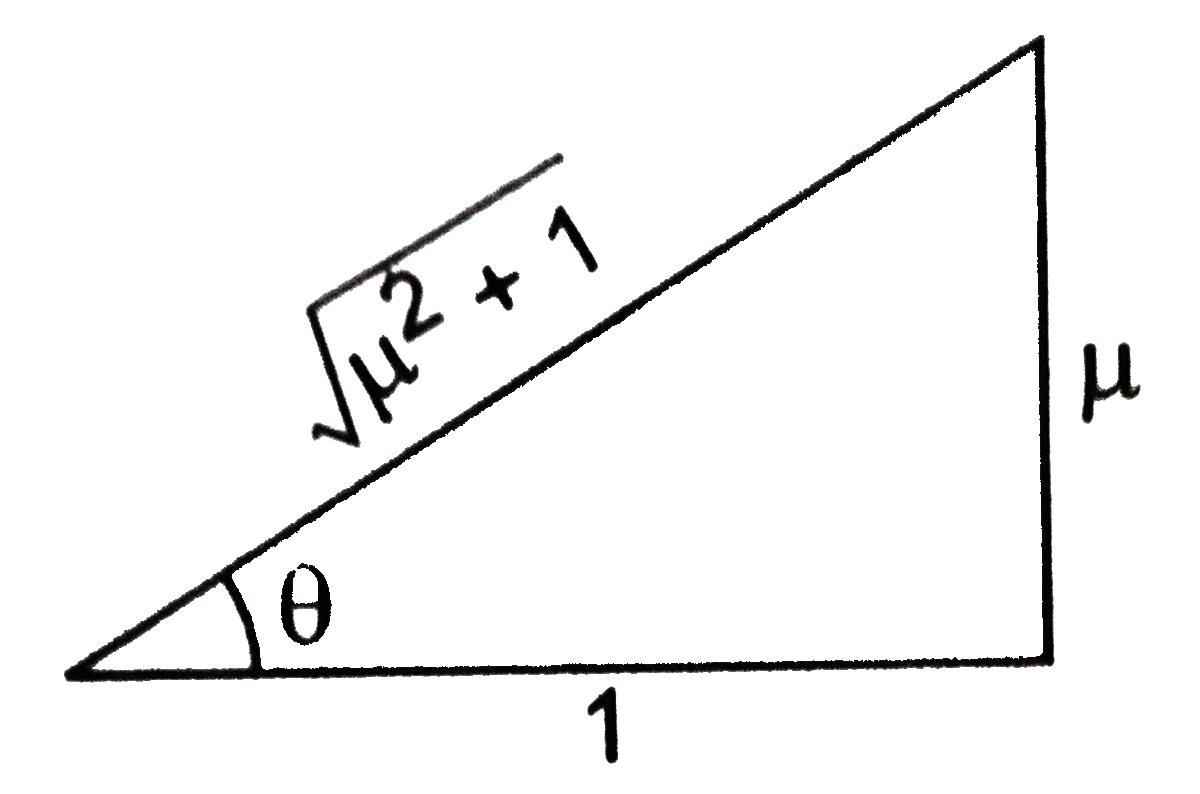 .
.