Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A sphere of mass 200 g is attached to an inextensible string of length...
Text Solution
|
- A sphere of mass 200 g is attached to an inextensible string of length...
Text Solution
|
- A sphere of mass 0.1kg is attached to an inextensible string of length...
Text Solution
|
- A particle of mass 21 g attached to a string of 70 cm length is whirle...
Text Solution
|
- 1 क्रिगा द्रव्यमान का एक गोला 50 सेमी लम्बी डोरी के एक सिरे पर बँधा है...
Text Solution
|
- 200 ग्राम का एक गोला 130 सेमी लम्बी डोरी के एक सिरे पर बंधा है जिसका द...
Text Solution
|
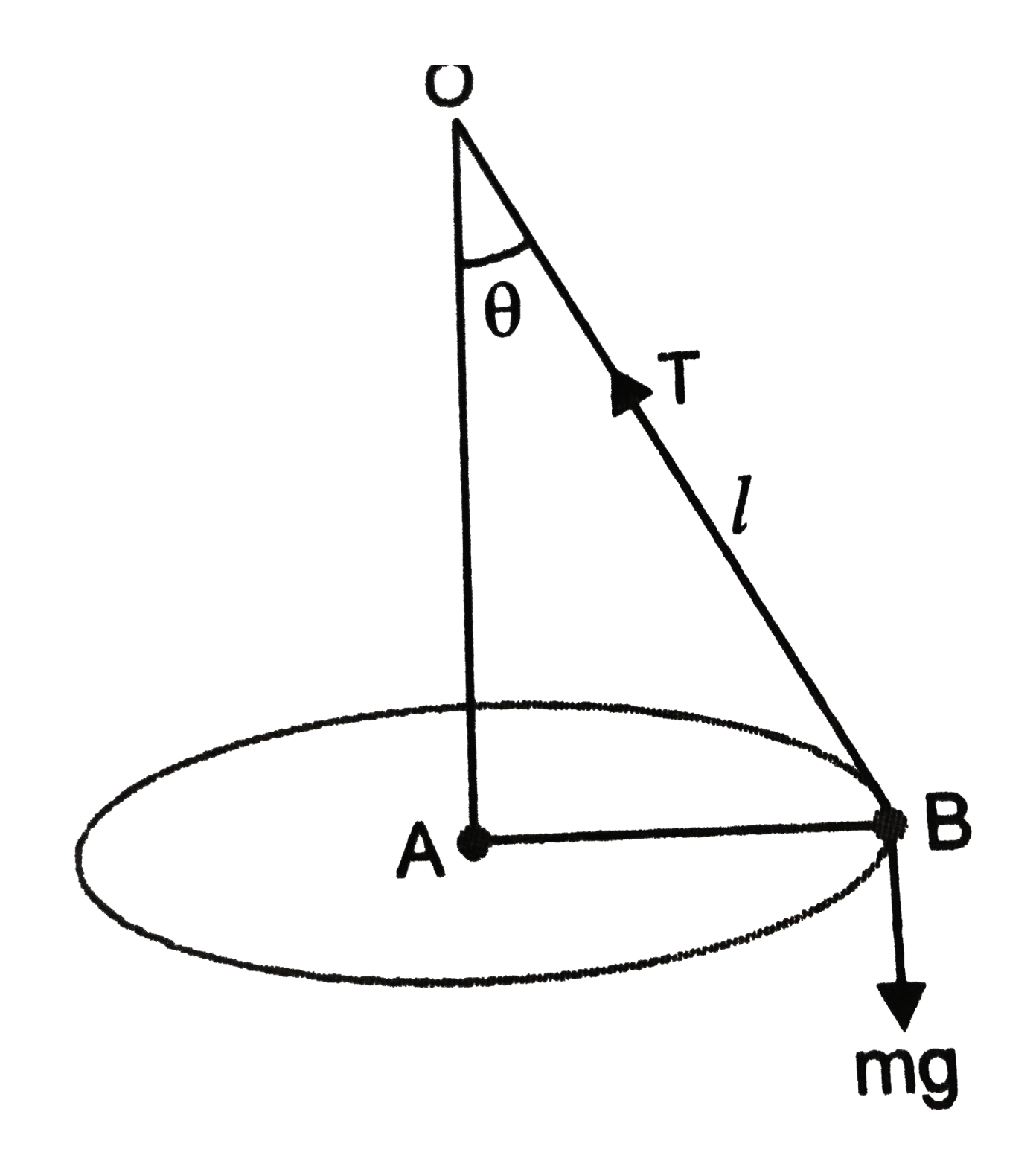
- A heavy small sized sphere is suspended by a string of length l . The ...
Text Solution
|
- A sphere of radius 25 cm and mass 1 kg is hung by a string of negligib...
Text Solution
|
- A sphere of mass 200 g remains suspended from a rigid support by means...
Text Solution
|
 .
.