Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Shown a smooth looping the loop track A particle of mass m is released...
Text Solution
|
- Shown a smooth looping the loop track A particle of mass m is released...
Text Solution
|
- An object of mass m is released from rest at a height h above the surf...
Text Solution
|
- A small block of mass m slides along a smooth track, as shown in fig. ...
Text Solution
|
- An inclined track ends in a circular loop of radius r. From what heigh...
Text Solution
|
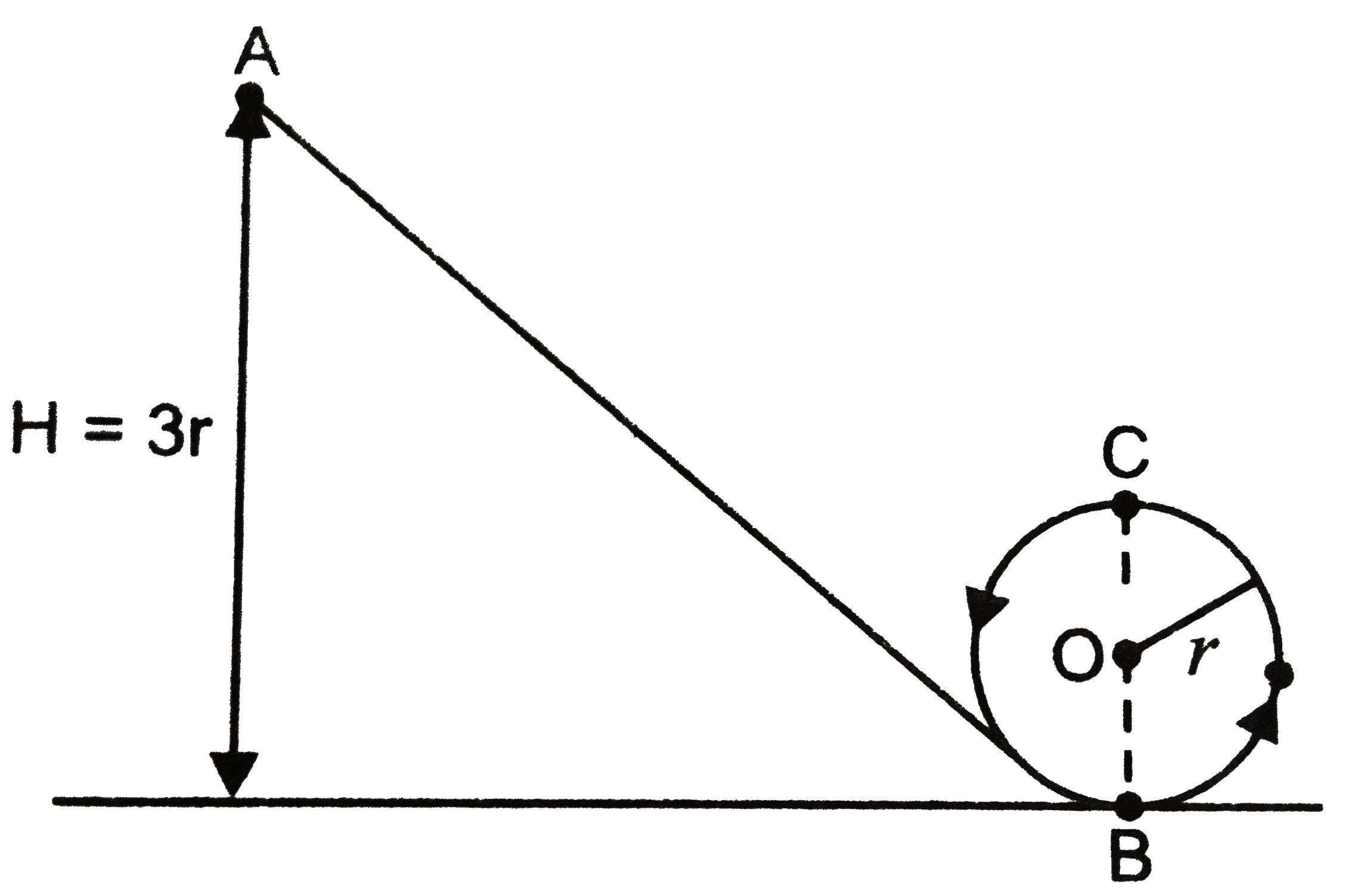
- A particle of mass m is released from point A as shown in the gigure. ...
Text Solution
|
- An inclined track ends in a circular loop of radius 'r'. From what hei...
Text Solution
|
- An inclined track ends is a circular loop of diameter D. From what hei...
Text Solution
|
- A small block of mass m slides along a smooth track as shown in the fi...
Text Solution
|
 .
.