Home
Class 11
PHYSICS
A thin rod of length 'L' is lying along ...

A thin rod of length 'L' is lying along the `x`-axis with its ends at `x=0` and `x=L` its linear (mass/length) varies with `x` as `k((x)/(L))^n`, where n can be zero of any positive number. If to position `x_(CM)` of the centre of mass of the rod is plotted against 'n', which of the following graphs best apporximates the dependence of `x_(CM)` on n?

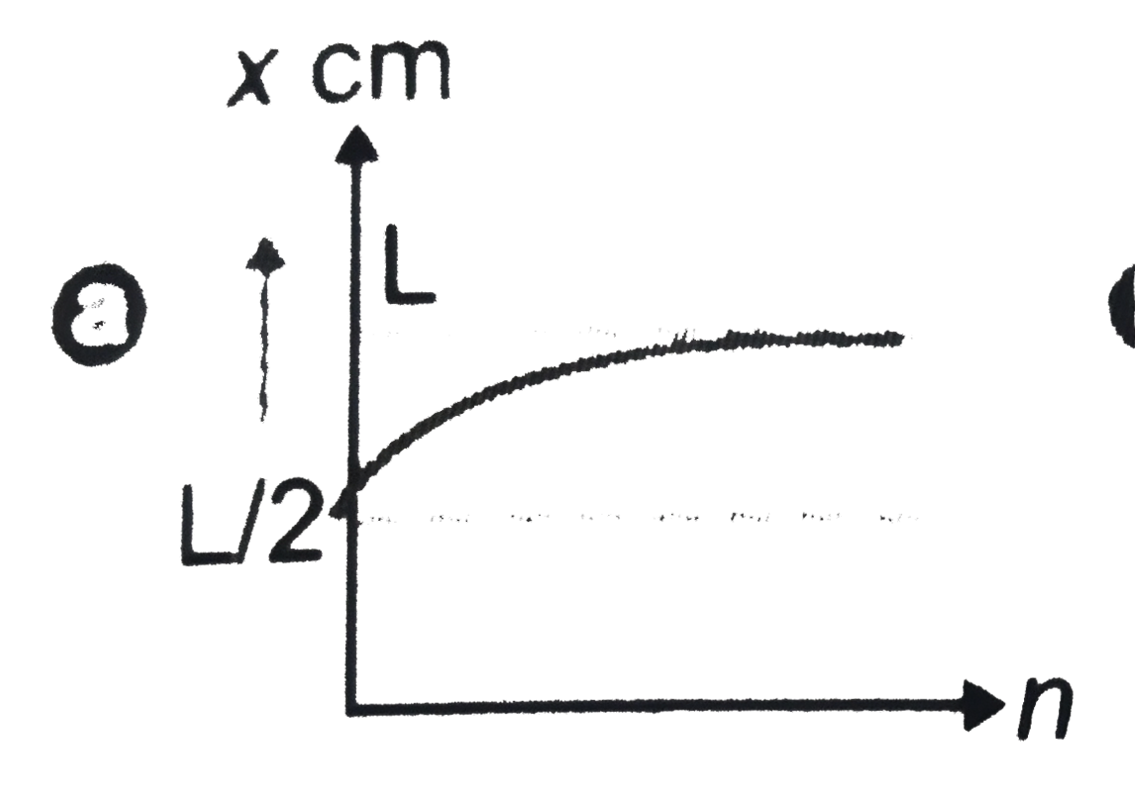
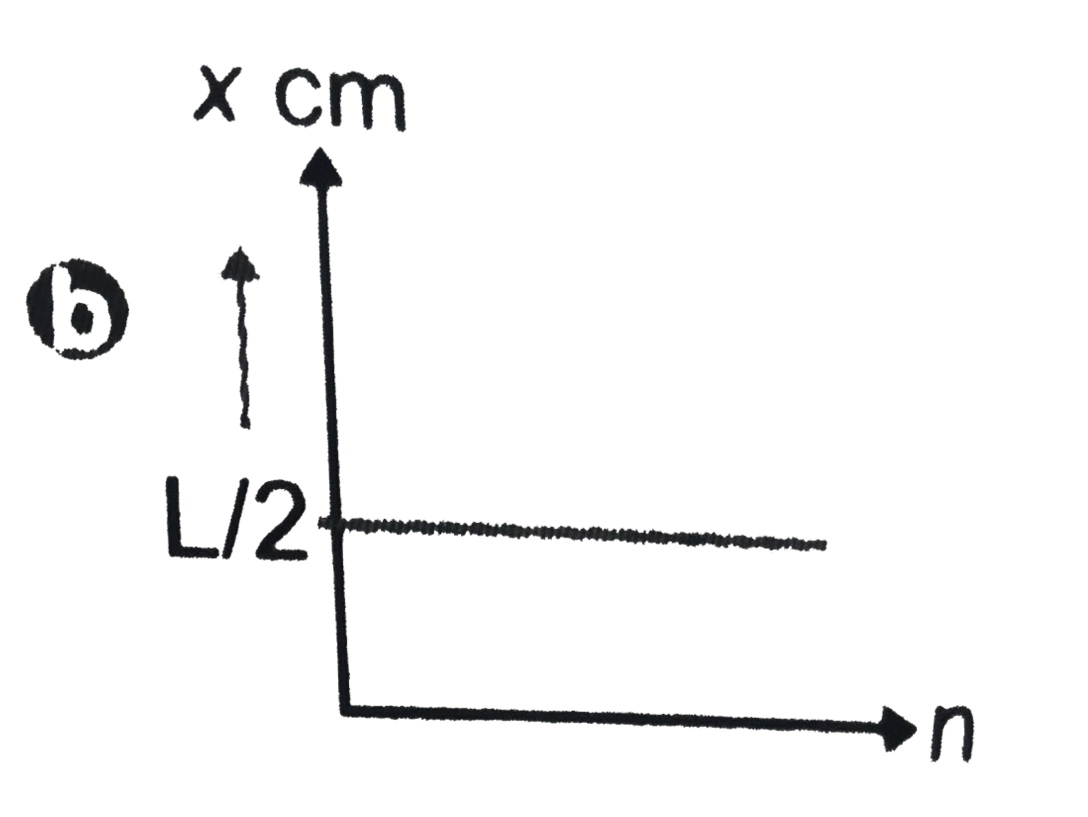
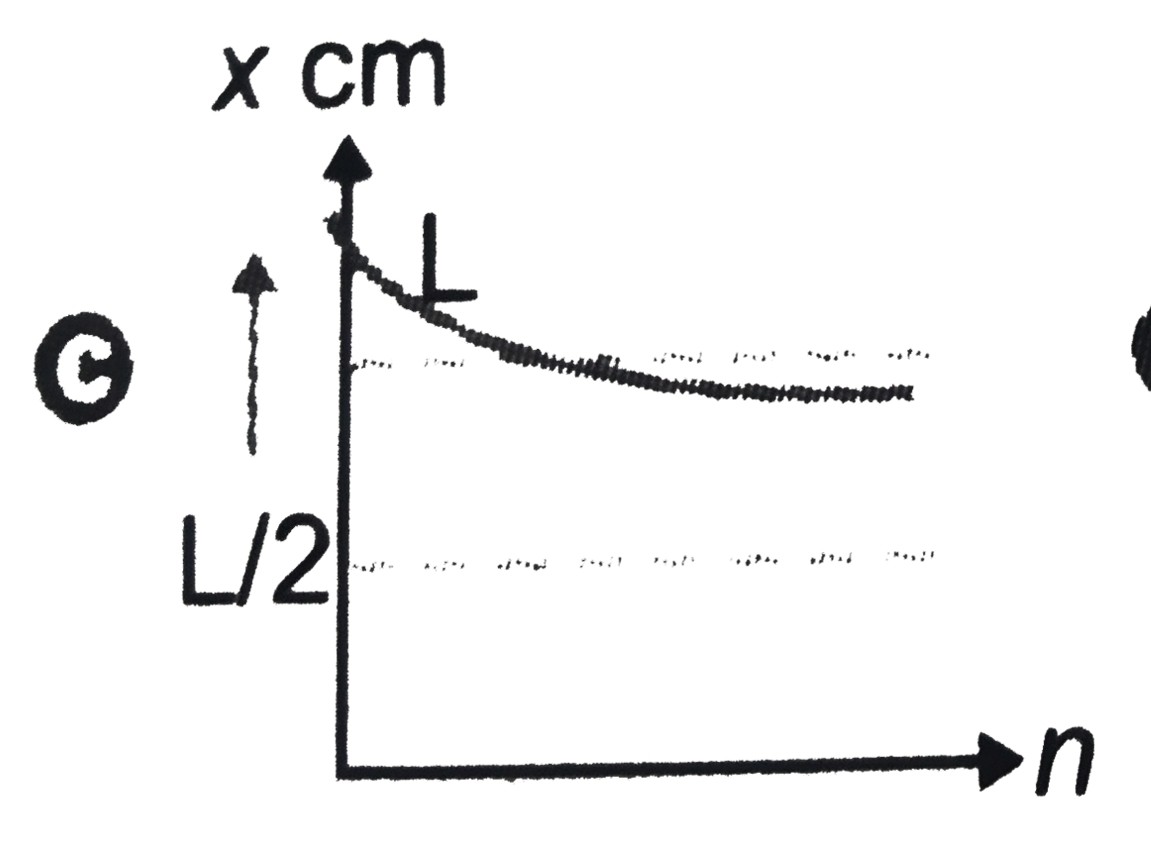
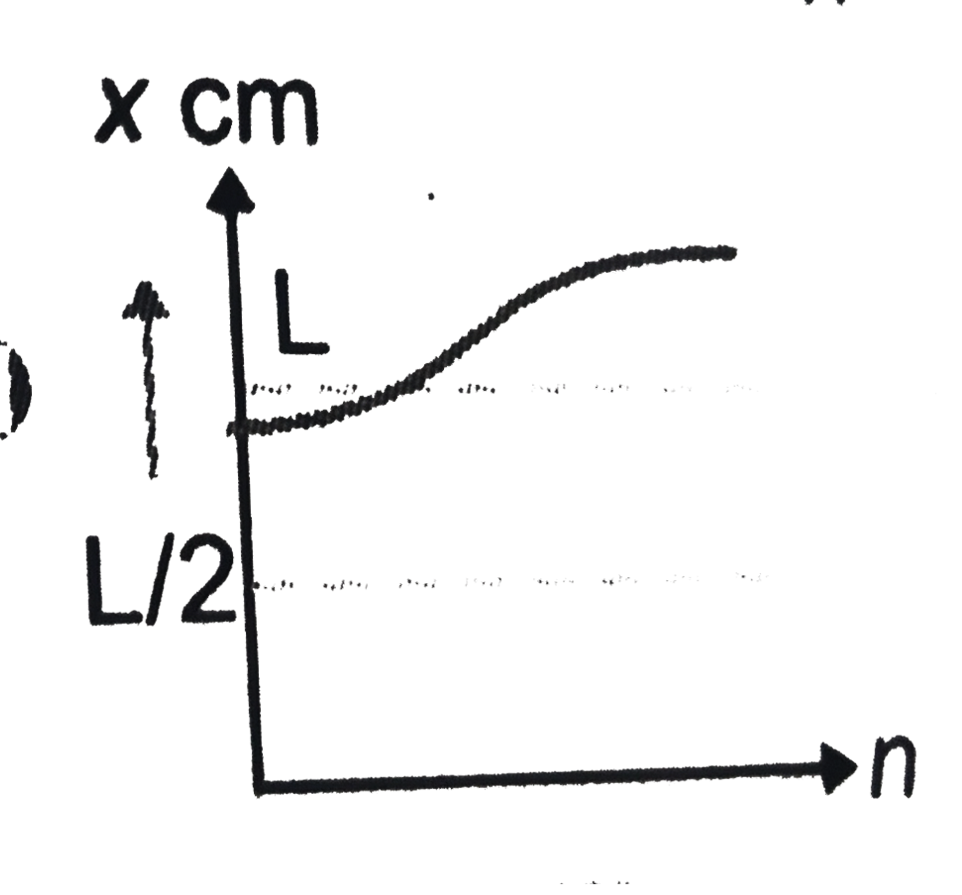
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A
Linear density `rho ( = "mass"//"length") = k ((x)/(L))^(n)`
when `n = 0, rho =` constant. The c.m will be at the centre of the ord, i.e. at `x = L//2`.
As n increases to 1, 2, 3,….,linear density goes on increasing. The c.m shifts beyond `x = L//2`, towards `x = L`. For sufficiently large values of n, the c.m tends to be at the other end `x = L` of the rod.
Graph (a) in Fig. is the best appoximation of dependence of `x_(cm)` on n.
Promotional Banner

Similar Questions

Explore conceptually related problems

A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as k((x)/(L))^n where n can be zero or any positive number. If the position X_(CM) of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of X_(CM) on n?

A thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx^(4) . Find the position of centre of mass of rod in meters.

A thin rod of length 6 m is lying along the x-axis with its ends at x = 0 and x = 6m . It linear density (mass/length) varies with x as kx^(4) . Find the position of centre of mass of rod in meters.

A rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/length) lamda of the rod varies with the distance x from the origin as lamda = Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.

A rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) lambda of the rod varies with the distance x from the origin as lambda = Rx . Here, R is a positive constant. Find the position of centre of mass of this rod.

A rod of length L is placed along the x-axis between x=0 and x=L . The linear mass density (mass/length) rho of the rod varies with the distance x from the origin as rho=a+bx . Here, a and b are constants. Find the position of centre of mass of this rod.

A rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is lambda such that lambda=a+bx . Find the mass of the rod.

A rod of length L is placed along the X-axis between x=0 and x=L . The linear density (mass/length) rho of the rod varies with the distance x from the origin as rhoj=a+bx. a. Find the SI units of a and b. b. Find the mass of the rod in terms of a,b, and L.

The mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is