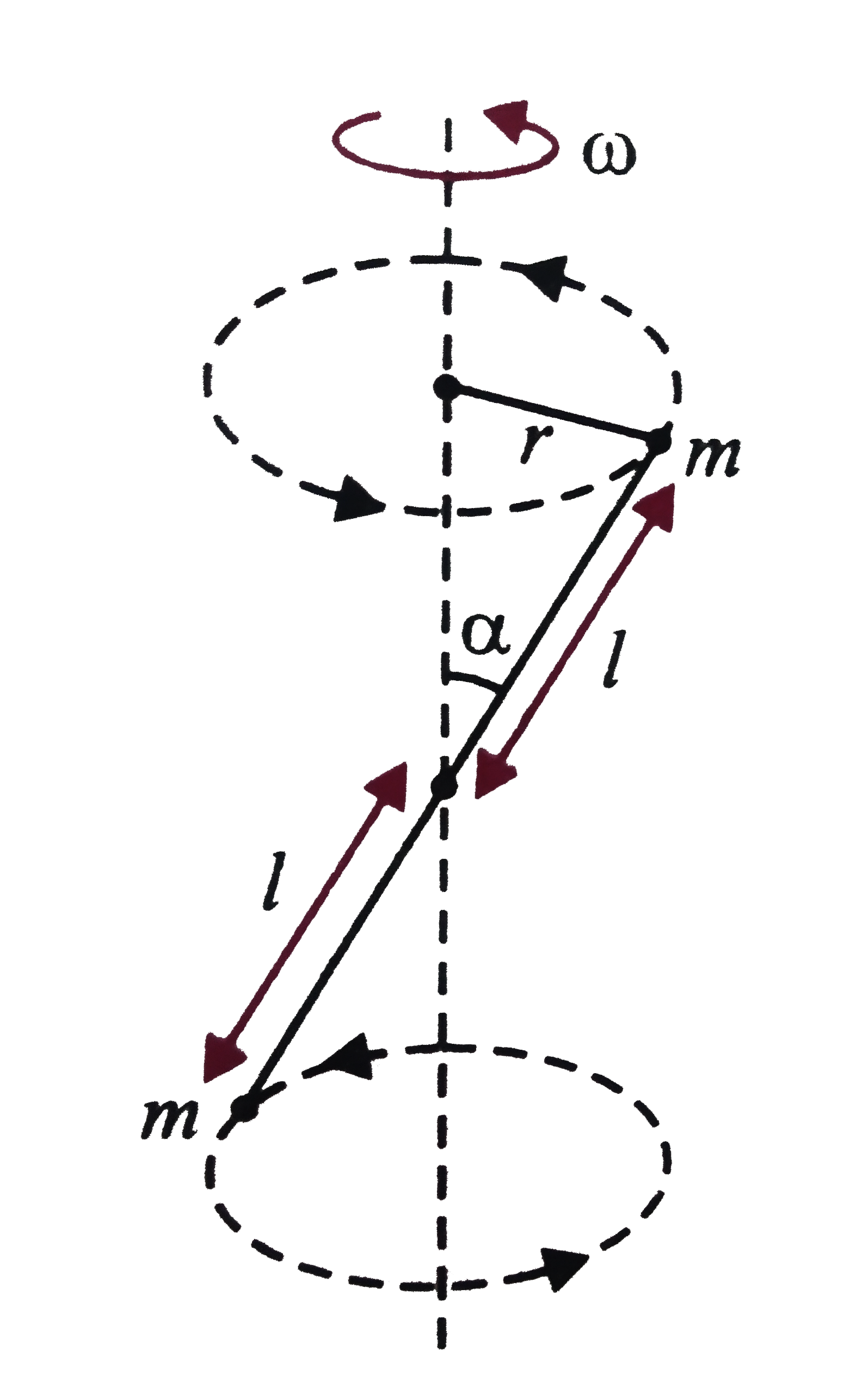
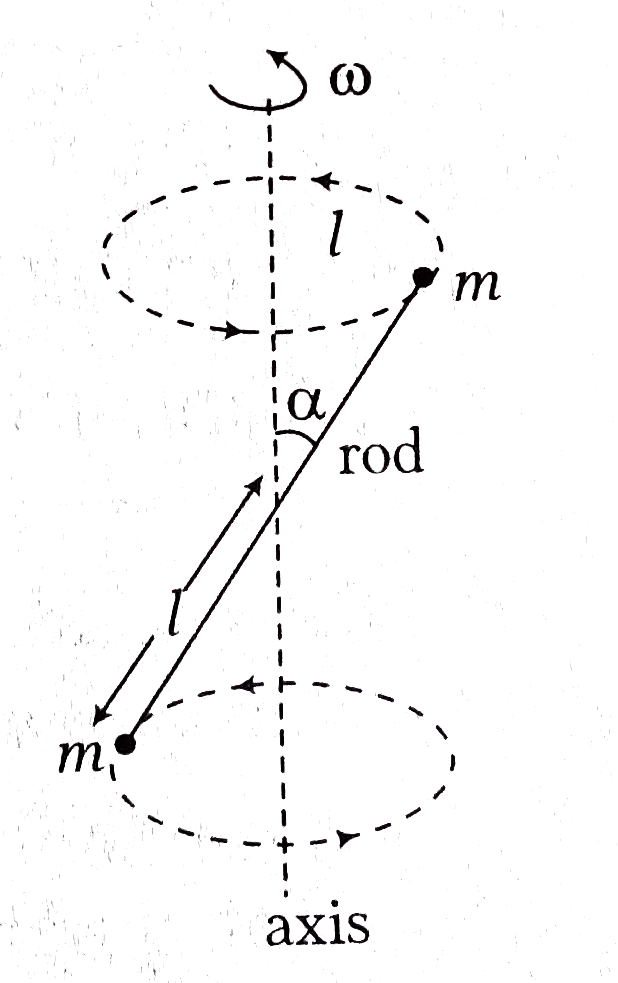A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A massless rod S having length 2l has equal point masses attached to i...
Text Solution
|
- Two particles , each of mass m and charge q, are attached to the two ...
Text Solution
|
- A massless rod S having length 2l has point masses attached to its two...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- AB is a mass less rigid rod of length 2l. It is free to rotate in vert...
Text Solution
|
- A uniform rod of mass m and length L is fixed to an axis, making an an...
Text Solution
|
- A massless rod S having length 2l has equal point masses attached to i...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- Find the moment of inertia of thin and massless rod about an axis pass...
Text Solution
|