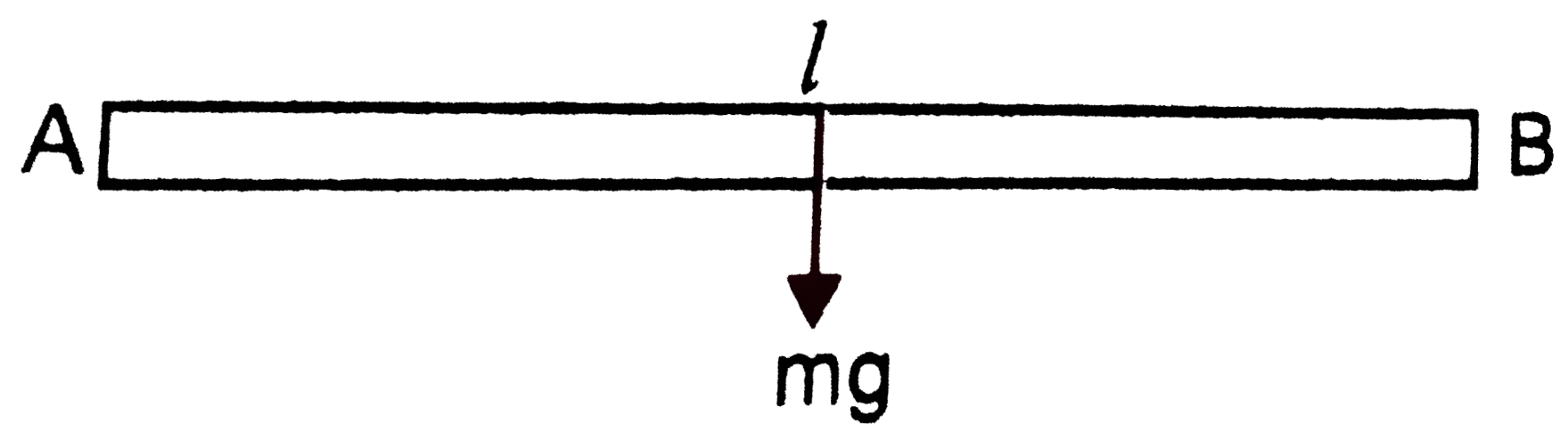
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A unifrom rod of length l and mass m is free to rotate in a vertical p...
Text Solution
|
- A unifrom rod of length l and mass m is free to rotate in a vertical p...
Text Solution
|
- A unifrom rod of length l and mass m is free to rotate in a vertical p...
Text Solution
|
- A uniform rod of length L and mass M is free to rotate about a frictio...
Text Solution
|
- The thin rod shown below has mases M and length L. A force F acts at o...
Text Solution
|
- A uniform rod AB of length l and mass m is free to rotate abou...
Text Solution
|
- एक समरूप छड़ AB की लम्बाई l तथा द्र्वयमान m है , यह बिंदु A के परित घूर...
Text Solution
|
- A uniform rod of length l and mass M pivoted about its end as shown in...
Text Solution
|
- A uniform rod AB of length l and mass m is free to rotate about point ...
Text Solution
|