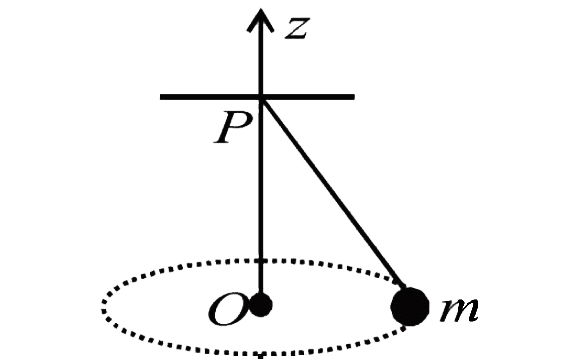
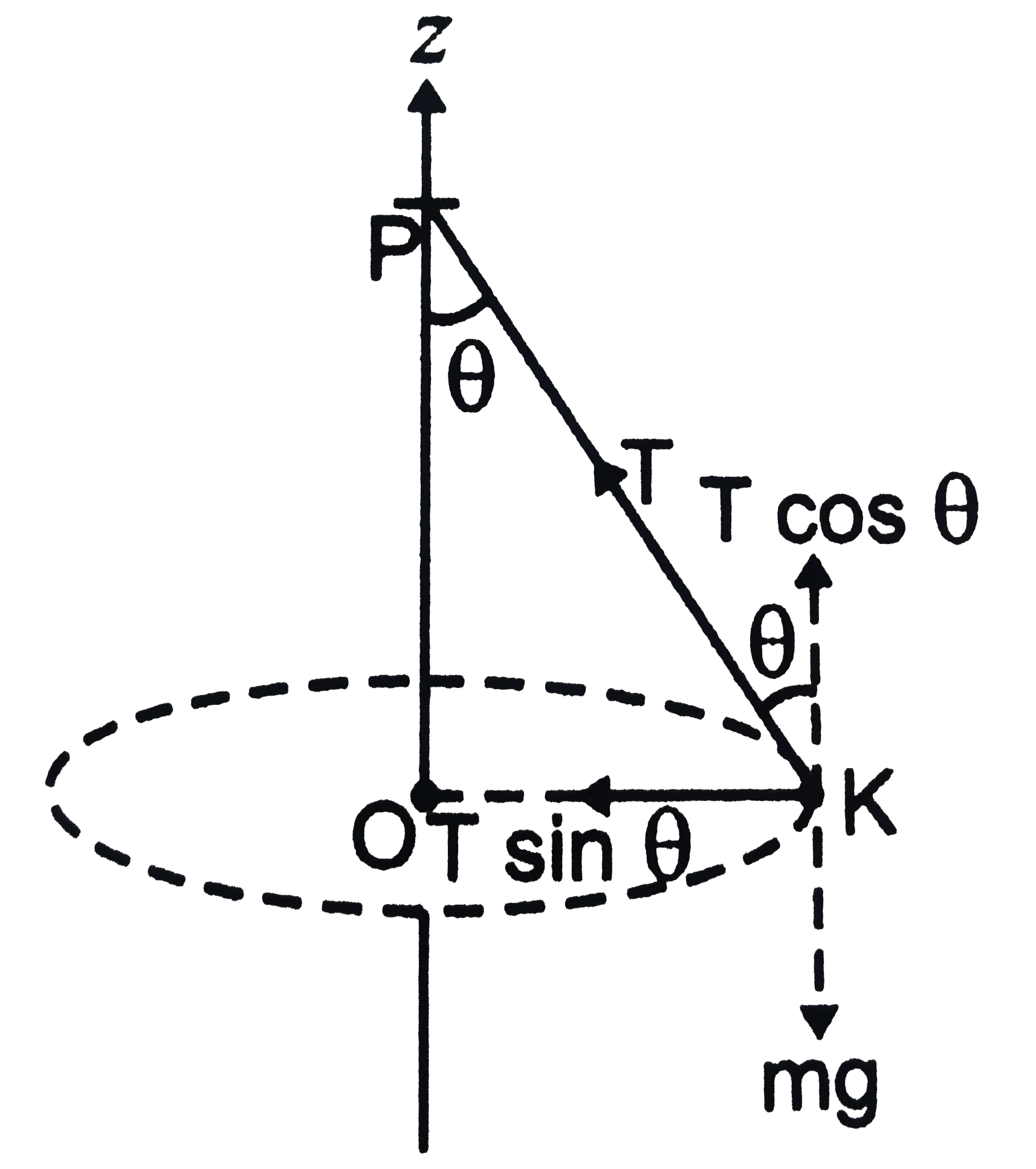
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small mass m is attached to a massless string whose other end is fi...
Text Solution
|
- Two particles of mass m each are attached to a light rod of length d, ...
Text Solution
|
- A small mass m is attached to a massless string whose other end is fi...
Text Solution
|
- A ring of mass M and radius R is rotating with angular speed omega abo...
Text Solution
|
- A mass m is attached to a rigid rod of negligible mass as shown in fig...
Text Solution
|
- A disc of mass M and radius R is rolling with angular speed w on horiz...
Text Solution
|
- एक छोटा पिंड m एक द्रव्यमान-रहित धागे से जुड़ा है। धागे का दूसरा सिरा ...
Text Solution
|
- The conical pendulum is in steady circular motion with constant angula...
Text Solution
|
- किसी भारहीन डोरी से छोटे से द्रव्यमान m को बाँध दिया जाता है जिसका दूस...
Text Solution
|