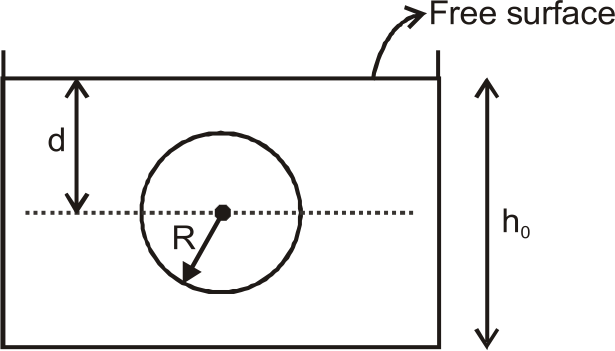
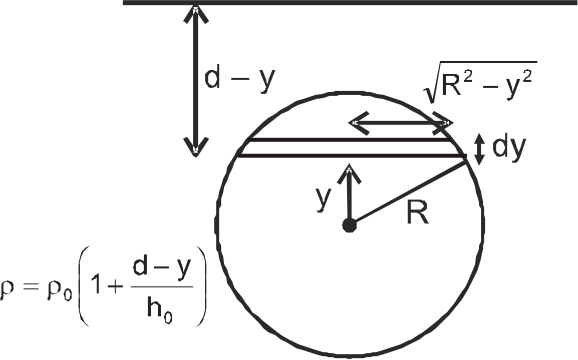
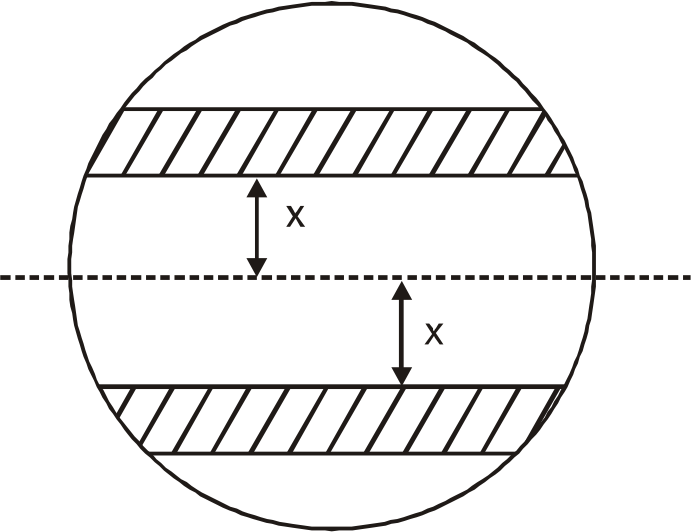
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-REVISION DPP-All Questions
- In a spring block system on a horizontal smooth surface. K = spring co...
Text Solution
|
- A container open from top, filled with water (density rhow) upto the t...
Text Solution
|
- A uniform solid sphere of radius R is in equilibrium inside a liquid w...
Text Solution
|
- A large open tank is filled with water upto a height H. A small hole i...
Text Solution
|
- A capillary tube with inner cross-section in the form of a square of s...
Text Solution
|
- A sphere of mass m and radius r is projected in a gravity free space w...
Text Solution
|
- A spherical ball of mass 4m, density sigma and radius r is attached to...
Text Solution
|
- In the figure shown, a light container is kept on a horizontal rough s...
Text Solution
|
- A cubical block of side a and density rho slides over a fixed inclined...
Text Solution
|
- A container filled with viscous liquid is moving vertically downwards ...
Text Solution
|
- The figure shows a soap film in which a closed elastic thread is lying...
Text Solution
|
- An isolated and charged spherical soap bubble has a radius 'r' and the...
Text Solution
|
- A cylinder with a movable piston contains air under a pressure p(1) a...
Text Solution
|
- The radius of a soap bubble is r. the surface tension of soap solution...
Text Solution
|
- A thin horizontal movable plate P is separated from two fixed horizon...
Text Solution
|
- A container of large uniform cross sectional area A resting on a horiz...
Text Solution
|
- In a certain gravity free space, the piston of an injection is being p...
Text Solution
|
- An external force 6N is applied on a sphere of radius R = 10 cm of mas...
Text Solution
|
- A block of density 2000kg//m^3 and mass 10kg is suspended by a spring ...
Text Solution
|
- Lower end of a capillary tube of radius 10^(-3) m is dipped vertically...
Text Solution
|