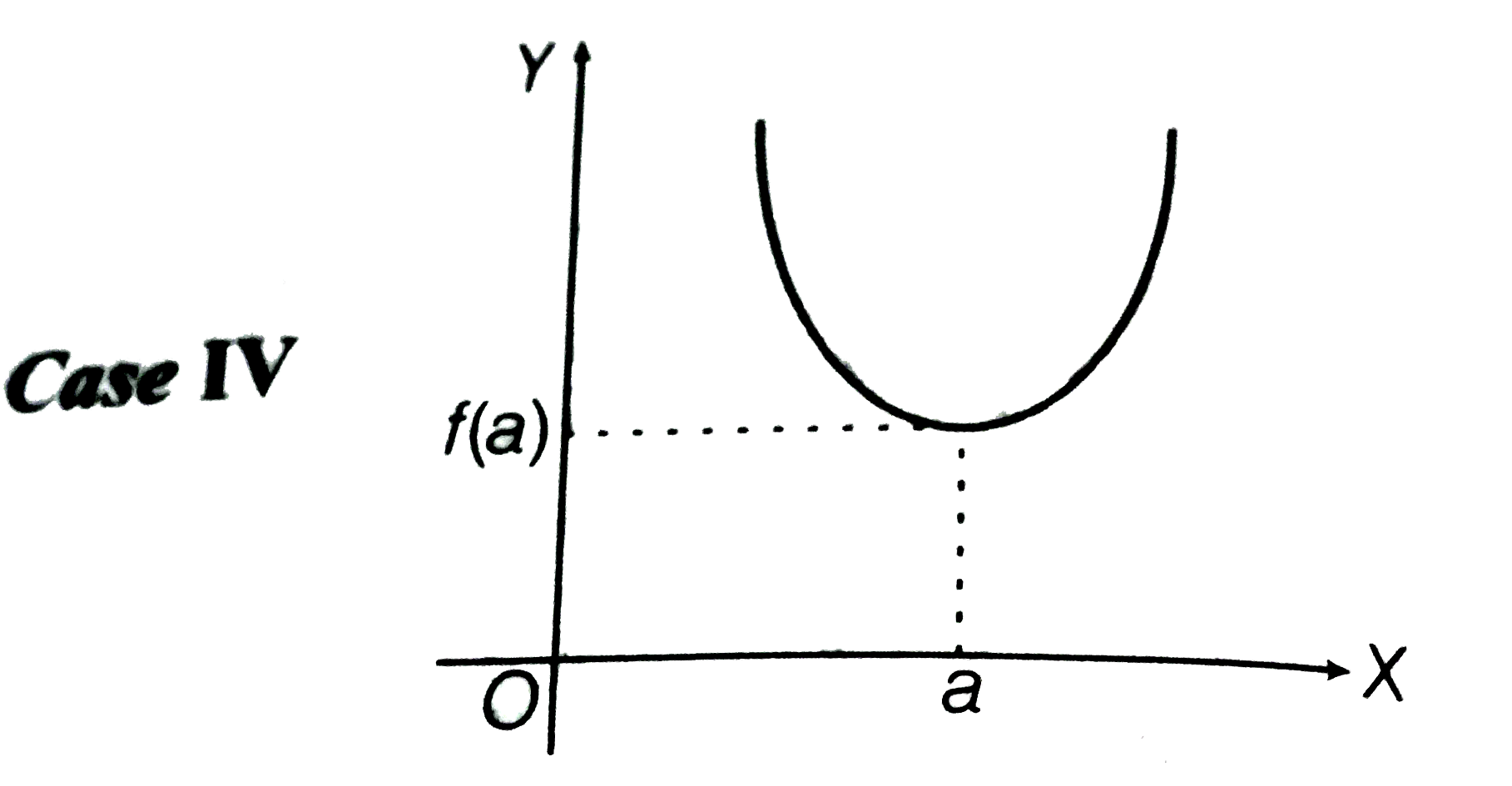
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LIMITS
ARIHANT MATHS|Exercise Exercise (Single Option Correct Type Questions)|40 VideosLIMITS
ARIHANT MATHS|Exercise Exercise (More Than One Correct Option Type Questions)|15 VideosINVERSE TRIGONOMETRIC FUNCTIONS
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|8 VideosLOGARITHM AND THEIR PROPERTIES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|4 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-LIMITS-Exercise For Session 6
- To evaluate lim(xtoa)[f(x)], we must analyse the f(x) in right hand ne...
Text Solution
|
- The value o lim(xtooo)(1/(n^(3)))([1^(2)x+1^(2)]+[2^(2)x+2^(2)]+…..+[n...
Text Solution
|
- The value of lim(xto1^(+))(int(1)^(x)|t-1|dt)/(sin(x-1)) is
Text Solution
|
- The value of lim(n->oo) sum(k=1)^n log(1+k/n)^(1/n),is
Text Solution
|
- Evaluate: (lim)(nvecoo)n[1/(n a)+1/(n a+1)+1/(n a+2)++1/(n b)]
Text Solution
|