Similar Questions
Explore conceptually related problems
Recommended Questions
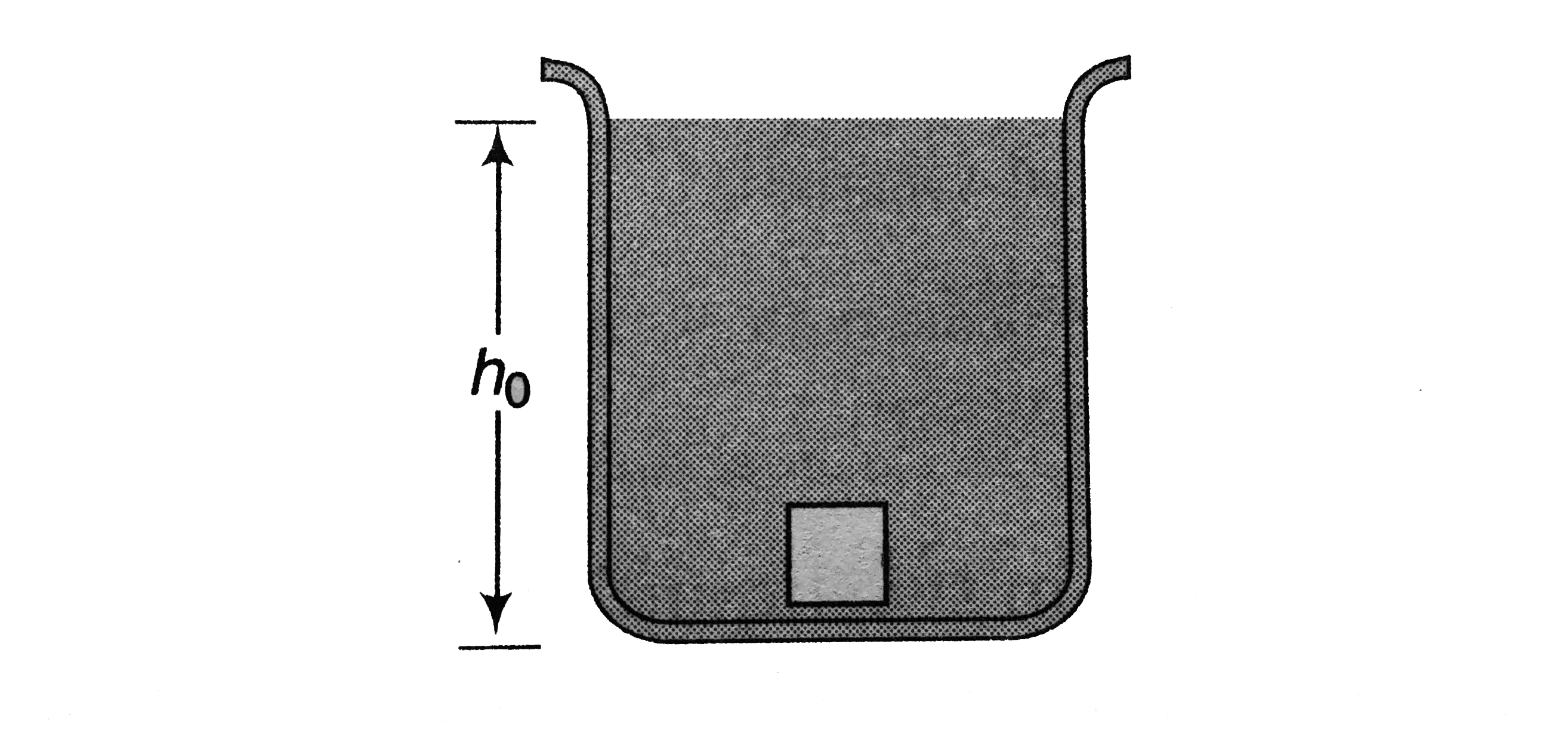
- Figure shown a container having liquid of variable density. The densit...
Text Solution
|
- A solid cube of side a and density rho(0) floats on the surface of a l...
Text Solution
|
- A block of material has a density rho(1) and floats three-fourth subme...
Text Solution
|
- Figure shown a container having liquid of variable density. The densit...
Text Solution
|
- A small spherical ball of radius r is released from its completely sub...
Text Solution
|
- A small spherical ball of radius r is released from its completely sub...
Text Solution
|
- A small spherical ball of radius r is released from its completely sub...
Text Solution
|
- Consider a solid cylinder of the density rho(s) cross section area A a...
Text Solution
|
- Density of a liquid varies with depth as rho=alpha h. A small ball of ...
Text Solution
|
 .
.