लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
रैखिक प्रोग्रामन
KC SINHA|Exercise दो चरों में एक रैखिक असमिका के हल पर आधारित प्रश्नः|4 Videosरैखिक प्रोग्रामन
KC SINHA|Exercise दो चरों में रैखिक असमिकाओं के निकाय के हल पर आधारित प्रश्नः|4 Videosयादृच्छिक चर और प्रायिकता बंटन
KC SINHA|Exercise Objective Questions|4 Videosरैखिक समीकरणों के निकाय का हल
KC SINHA|Exercise Objective Questions|4 Videos
KC SINHA-रैखिक प्रोग्रामन-OBJECTIVE QUESTIONS
- एक दूकानदान दो सामानों थर्मस फ्लास्क और वायुशून्य बर्तनों को बेचता है।...
Text Solution
|
- The corner pont sof the feasible region determined by the followign sy...
Text Solution
|
- The maximum value of z=x+3y such that 2x+yle20,x+2yle20,xge0,yge0 is
Text Solution
|
- The maximum valueof z=6x+8y subjected to constraings 2x+yle30, x+2yle2...
Text Solution
|
- By graphical method, the solutionn of the linear programming problem. ...
Text Solution
|
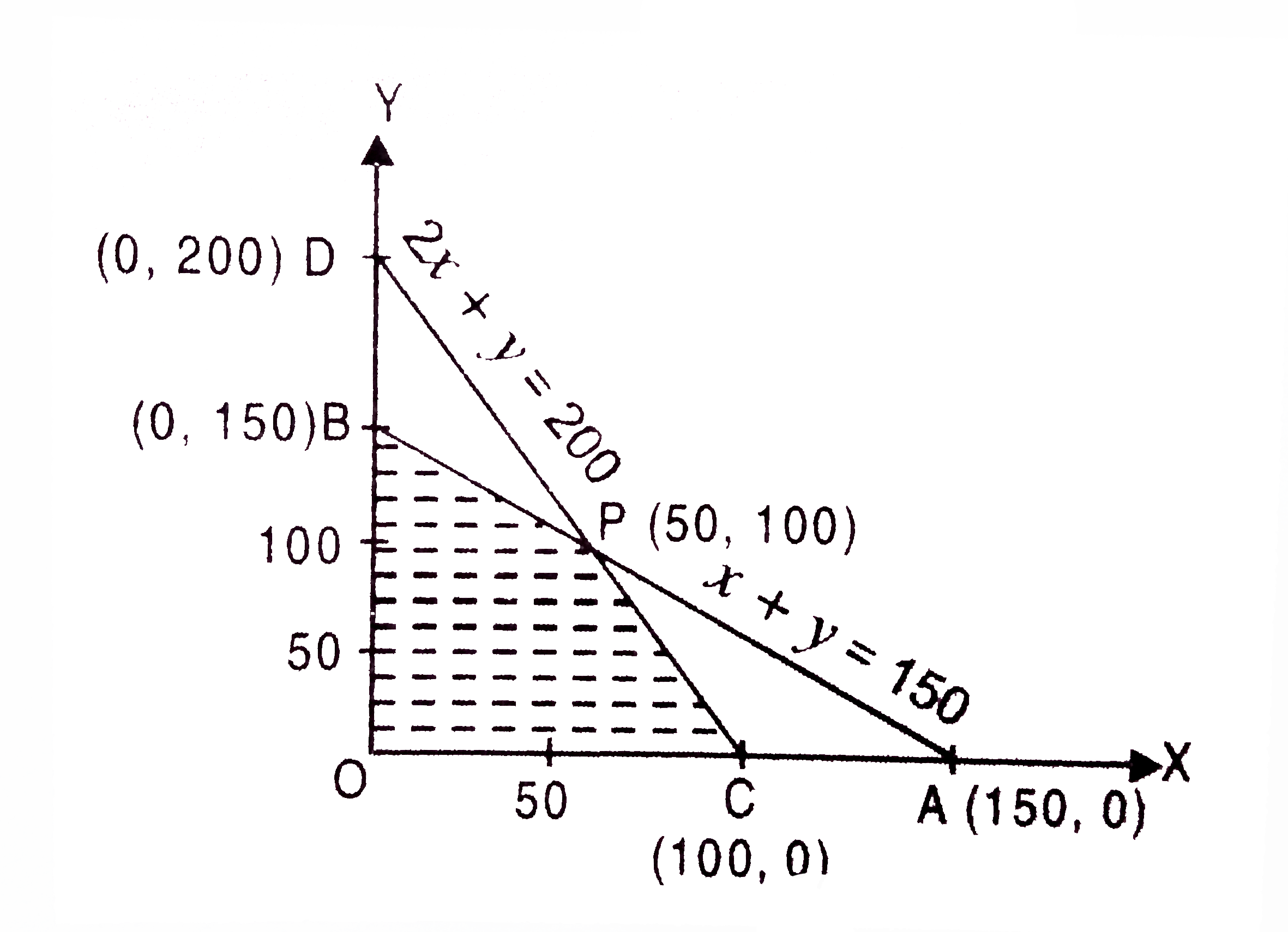
- Shaded region is represented by
Text Solution
|