Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PROBABILITY
TARGET PUBLICATION|Exercise Practice set 5.3|1 VideosPROBABILITY
TARGET PUBLICATION|Exercise Practice Set 5.4|5 VideosPROBABILITY
TARGET PUBLICATION|Exercise Practice Set 5.1|1 VideosMODEL QUESTION PAPER (PART - II)
TARGET PUBLICATION|Exercise Questions|28 VideosPYTHAGORAS THEOREM
TARGET PUBLICATION|Exercise Chapter Assessment|16 Videos
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-PROBABILITY-Practice set 5.2
- For each of the following experiments, write the sample space S and th...
Text Solution
|
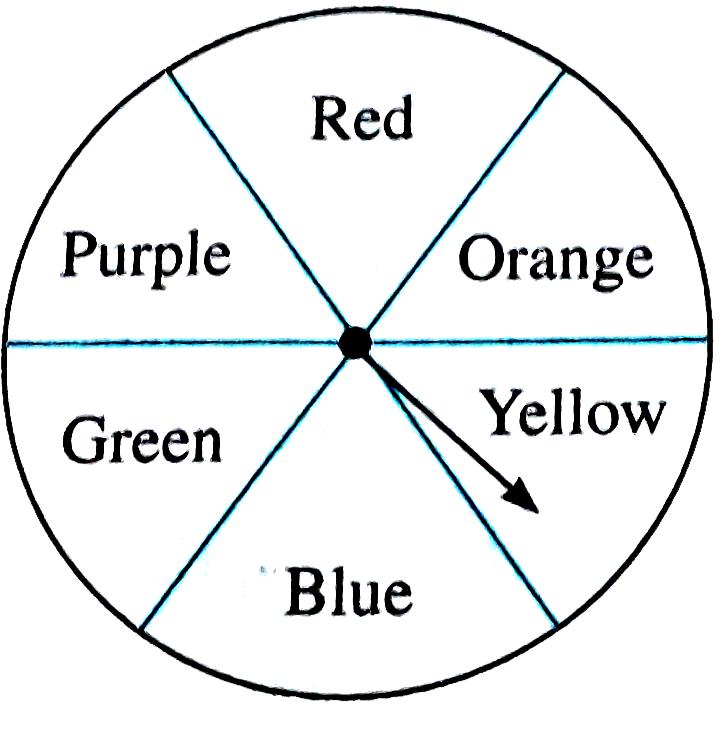
- The arrow is rotated and it stops randomly on the disc. Find out on wh...
Text Solution
|
- In the month of March 2019, find the days on which the date is a multi...
Text Solution
|
- Form a 'Road sefety committee' of two, from 2 boys (B(1),B(2)) and ...
Text Solution
|