Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMILARITY
TARGET PUBLICATION|Exercise Try this|1 VideosSIMILARITY
TARGET PUBLICATION|Exercise Practice Set 1.1|8 VideosSIMILARITY
TARGET PUBLICATION|Exercise Chapter Assessment|19 VideosQUESTION FROM STD. IX
TARGET PUBLICATION|Exercise Statistics|14 VideosSTATISTICS
TARGET PUBLICATION|Exercise Problem Set-6|21 Videos
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-SIMILARITY -Textual Activity
- Draw a Delta ABC. 1.Bisect angleB and name the point of intersection...
Text Solution
|
- Draw three parallel lines. ii.Label them as l, m, n. iii.Draw tran...
Text Solution
|
- In the adjoining figure, AB abs() CD abs() EF. If AC = 5.4, CE = 9, BD...
Text Solution
|
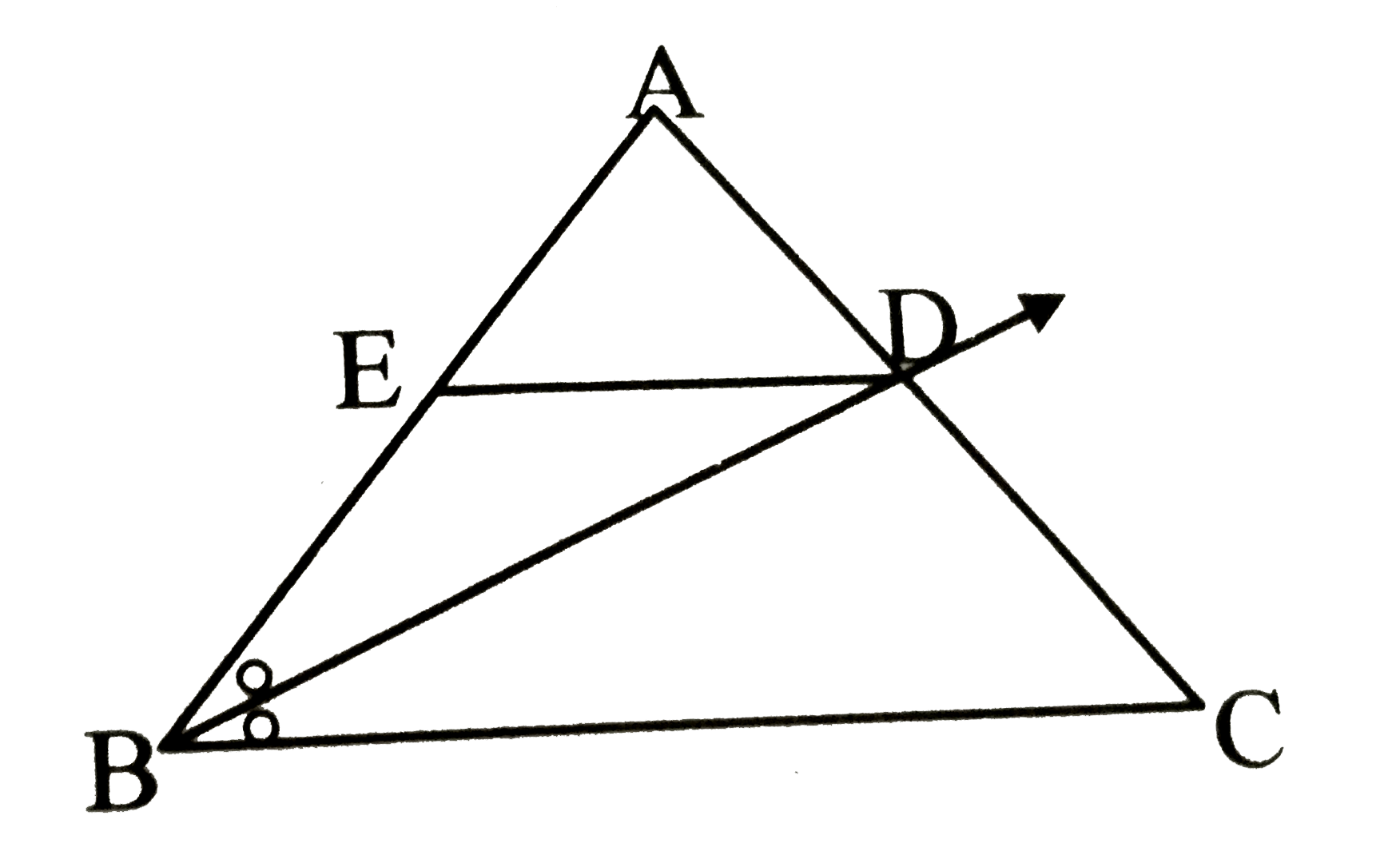
- In Delta ABC, ray BD bisects angleABC. A-D-C, side DEabs()side BC, A-E...
Text Solution
|