Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMILARITY
TARGET PUBLICATION|Exercise Practice Set 1.3|9 VideosSIMILARITY
TARGET PUBLICATION|Exercise Practice Set 1.4|7 VideosSIMILARITY
TARGET PUBLICATION|Exercise Practice Set 1.1|8 VideosQUESTION FROM STD. IX
TARGET PUBLICATION|Exercise Statistics|14 VideosSTATISTICS
TARGET PUBLICATION|Exercise Problem Set-6|21 Videos
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-SIMILARITY -Practice Set 1.2
- Given below are some triangle and lengths of line segments. Identify i...
Text Solution
|
- In DeltaPQR, PM=15, PQ=25, PR=20, NR=8. State whether line NM is paral...
Text Solution
|
- In DeltaMNP, NQ is a bisector of /N. If MN=5, PN=7, MQ=2.5, the find Q...
Text Solution
|
- Measures of same angles in the figure are given. Prove that (AP)/(PB)=...
Text Solution
|
- In trapezium ABCD side AB|| side PQ|| side DC, AP=15, PD=12, QC=14, fi...
Text Solution
|
- Find QP using given information in the figure.
Text Solution
|
- In the adjoining figure, if AB abs() CD abs() FE, then find x and AE.
Text Solution
|
- In DeltaLMN, ray MT bisects /LMN. If LM=6, MN=10. TN=8 then find LT.
Text Solution
|
- In DeltaABC set BD bisects /ABC. If AB-x, BC=x+5, AD=x-2, DC=x+2, then...
Text Solution
|
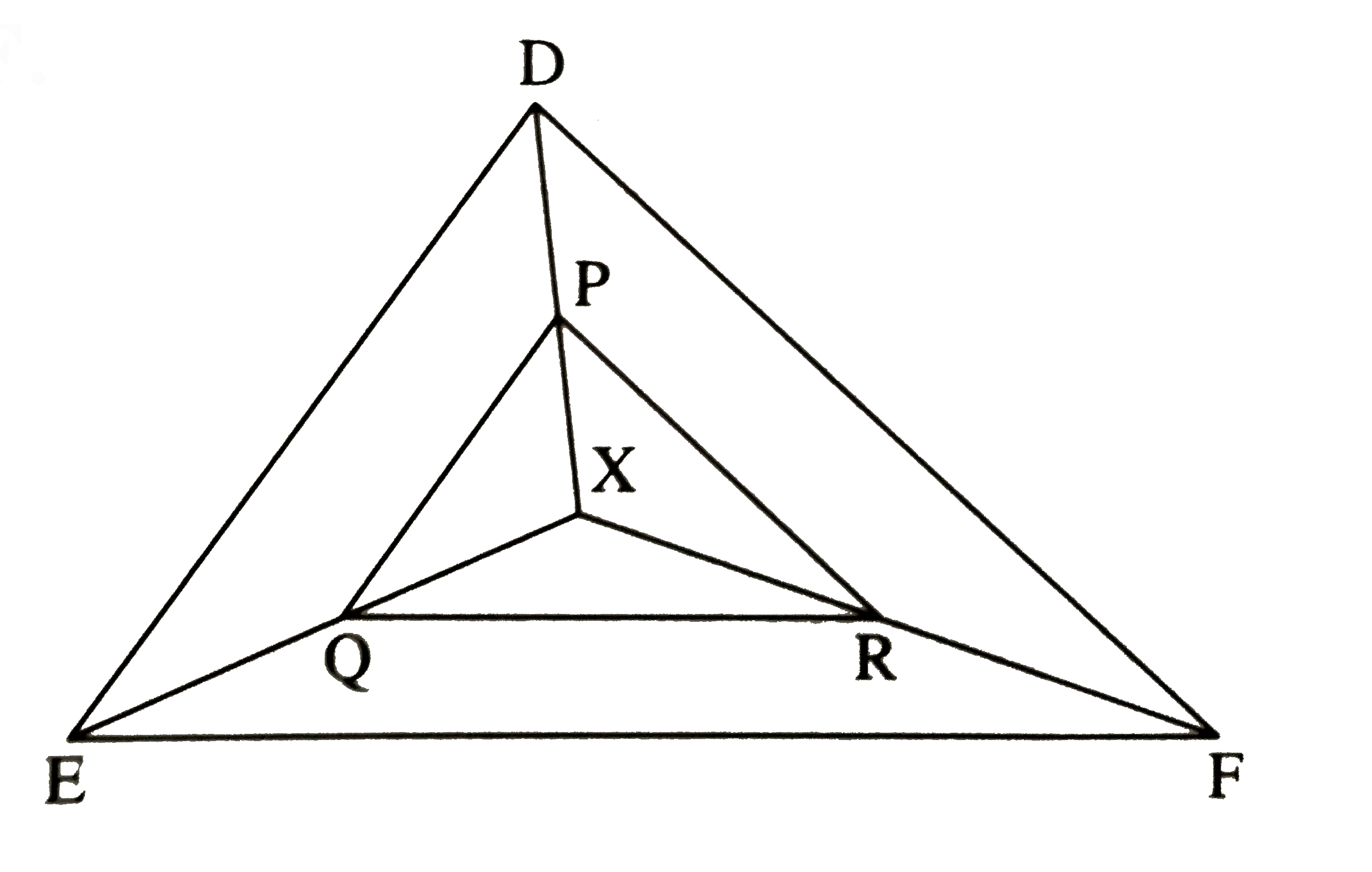
- In the figure X is any point in the interior of triangle. Point X is j...
Text Solution
|
- In DeltaABC,ray BD bisects angleABC and ray CE bisects angleACB. If se...
Text Solution
|