Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLE
TARGET PUBLICATION|Exercise Problem Set-3|25 VideosCIRCLE
TARGET PUBLICATION|Exercise Activities for Practice|4 VideosCIRCLE
TARGET PUBLICATION|Exercise Practice Set 3.4|6 VideosCHALLENGING QUESTIONS
TARGET PUBLICATION|Exercise Chapter 6: Statistics|4 VideosCO-ORDINATE GEOMETRY
TARGET PUBLICATION|Exercise CHAPTER ASSESSMENT|19 Videos
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-CIRCLE-Practice Set 3.5
- In the figure, ray PQ touches the circle at point Q. If PQ =12, PR = 8...
Text Solution
|
- In the figure, chord MN and chord RS intersect at point D. (1) If RD...
Text Solution
|
- In the figure, O is the centre of the circle and B is a point of conta...
Text Solution
|
- In the adjoining figure , if PQ=6,QR=10,PS=8 , find TS.
Text Solution
|
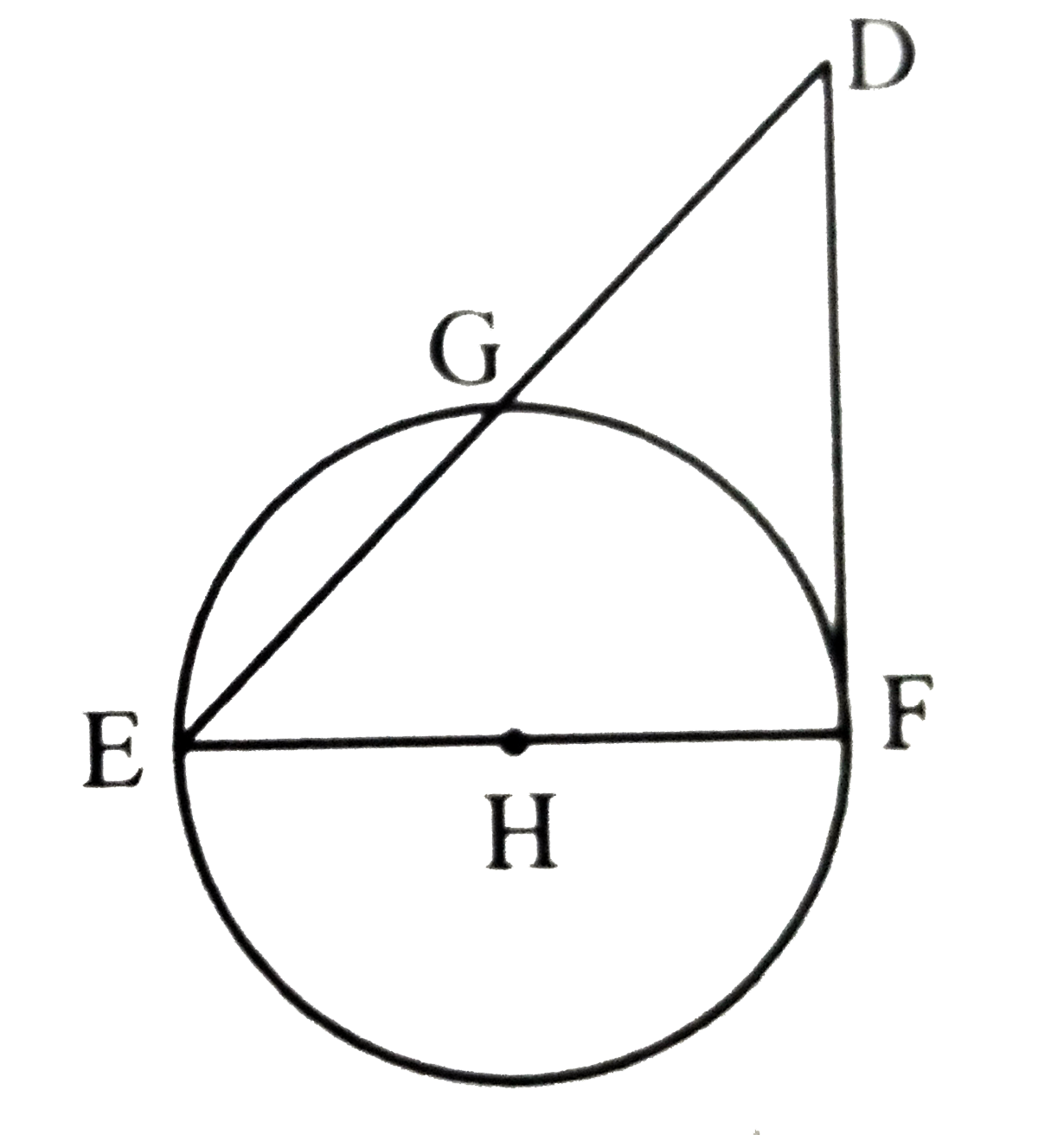
- In the adjoining figure , seg EF is a diameter and seg DF is a tangent...
Text Solution
|