Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-CIRCLE-Chapter Assessment
- If two circles with diameter 8cm and 6 cm touch externally, then the d...
Text Solution
|
- In the given figure , O is the centre of the circle. If m(arc AXB)=80^...
Text Solution
|
- In the given figure ,secants AP and CP intersect in point P. If AP=12,...
Text Solution
|
- Find the radius of the circle passing through the vertices of a right ...
Text Solution
|
- In the following figure, a tangent segment PA touching a circle in A a...
Text Solution
|
- In the given figure, Q is the centre of the circle and PM ,PN are tang...
Text Solution
|
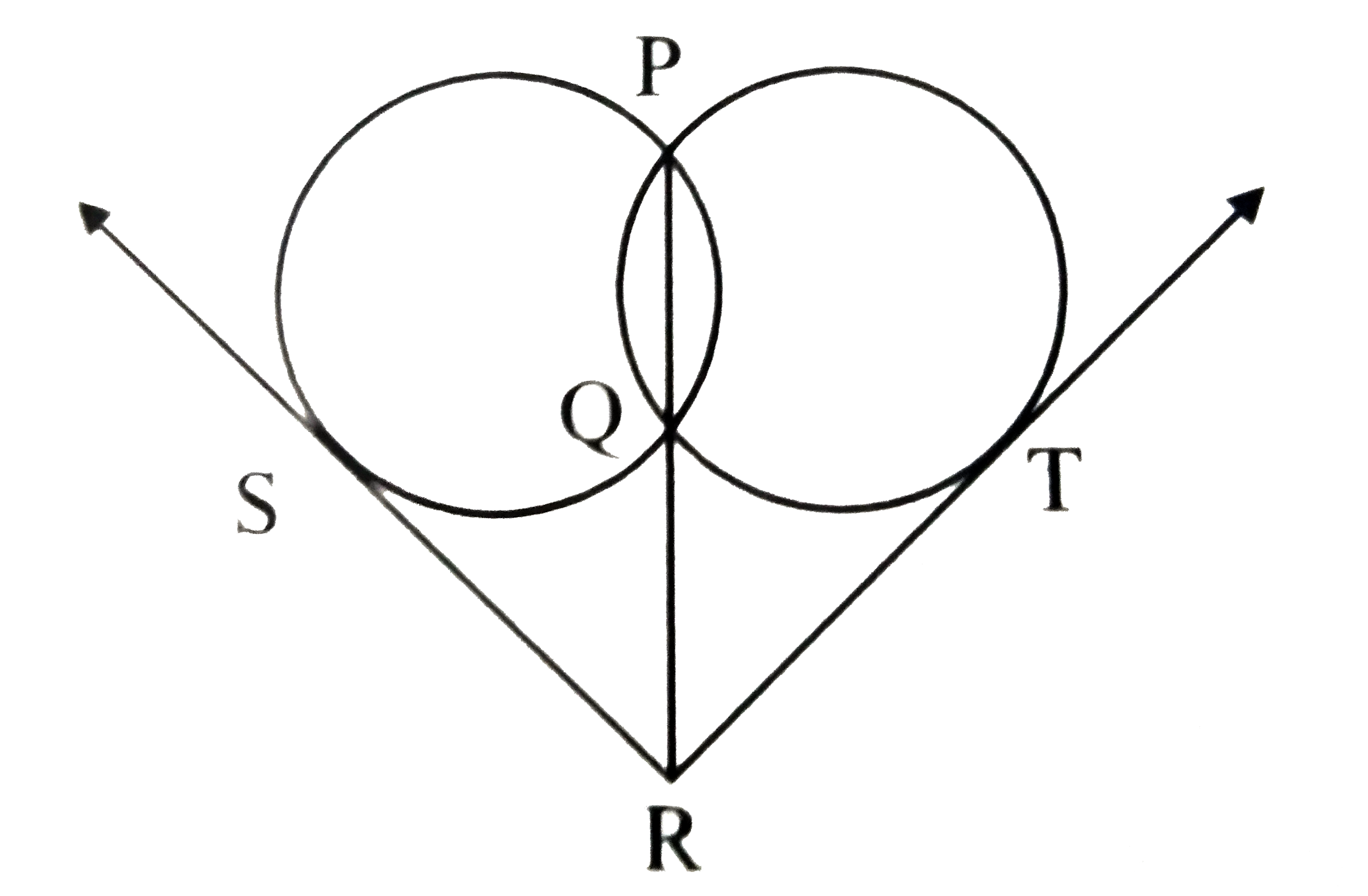
- In the figure, two circles intersect each other in points P and Q. If ...
Text Solution
|
- In the given figure, points S,T and U are the midpoints of sides PQ,QR...
Text Solution
|
- Prove that the opposite sides of a quadrilateral circumscribing a circ...
Text Solution
|