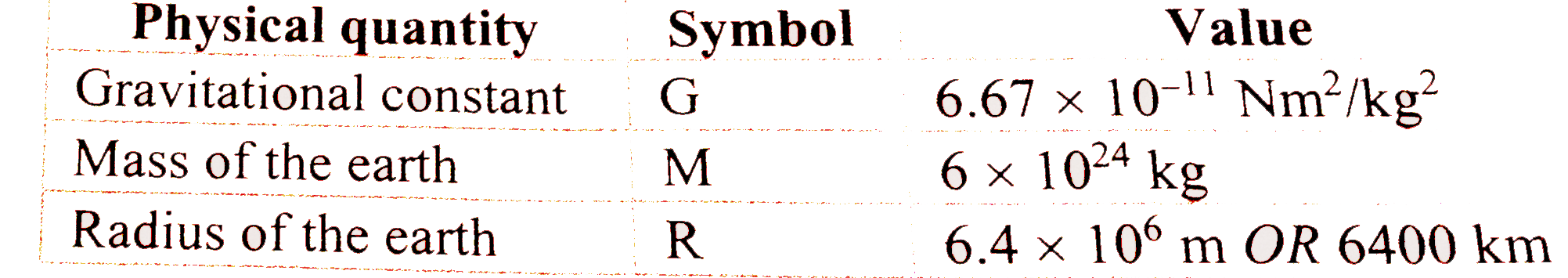Analyse
Step 1: Analyse the given data in the problem and find out what needs to be calculated.
Given : Height from the surface of the earth =20200 km = `2.02xx10^(7)m`
Also we know values of the basic physical constants like G,M and R :
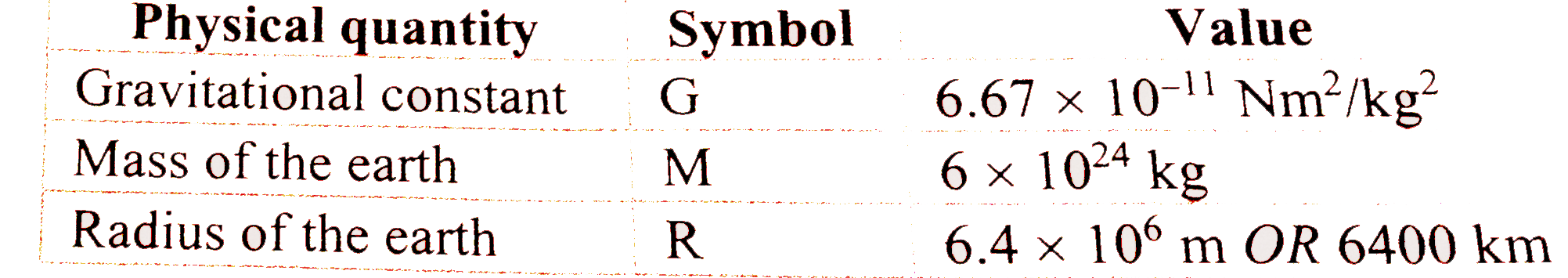
To find . (i) Tangential velocity `(v_(c))`
(ii) Time period of satellite (T)
Solve
Step 2: Write the formula foe tangential velocity,
`v_(c)=sqrt((GM)/(r))" " (i)`
Before getting started with tedious calcutions , first calculate the radius of the orbit from the centre of the earth.
R is the radius of the earth . As shown in figure ,the radius of the orbit 'r' is (R+H).
`therefore" " r=R+H=6400+20200=26600"km"=2.66xx10^(7)m`
Step 3 : Using equation (i) and substituing know values,
`v_(c)=sqrt((6.67xx10^(-11)xx6xx10^(24))/(2.66xx10^(7)))`
Step 4 : Separate the powers of 10 for simplification .
`thereforev_(c)=sqrt((6.67xx6)/(2.66)xx10^(6))`
For further simplification of calculation , take approximate values and contiue calcution.
`v_(c)~~sqrt((7xx6)/(3)xx10^(6))=sqrt(7xx2)xx10^(3)=sqrt(4)xx10^(3)`
Step 5 : As, 14 is not a perfect square we again use approximation for arriving at the final answer. ltbrlt Find out the upper and lower perfect squares near the required number.
Here, these values would be 9 and 16 . Hence our answer lies somewhere between 3 and 4 Also , 14 is much closer to 16 as compared to 9 which leads us to conclude the approximate value of `sqrt(14)~~3.8.`
`therefore" " v_(c)=3.8xx10^(3)"m/s"or3.8"km/s"`
Step 6 : To complete one revolution around the earth , the satellite travels distance equal to circumference of the orbit.
`therefore" Here,velocity"(v_(c))=("distance")/("time")=(2pir)/(T)rArrT=(2pir)/(v_(c))`
`therefore" " T=(2xx3.14xx2.66xx10^(7))/(3.8xx10^(3))`
Using approximations, .
`T~~=(2xx3xx3)/(4)xx10^(4)=4.5xx10^(4)s`
To convert the time in hours , divide the answer with 3600,
`T=(45000)/(3600)=(25)/(2)=12.5"hours"`
Answer check
without approximation , the answers to velocity of satellite and its time period will be as follows,
`v_(c)=sqrt((6.67xx10^(-11)xx610^(24))/(2.66xx10^(7)))=3878.8"m/s "or3.88" km/s"`
`T=(2xx3.14xx2.66xx10^(7))/(3.88xx10^(3))=43053s=11.96 "hours"`