Home
Class 10
PHYSICS
Observe the following diagram and answer...

Observe the following diagram and answer the questions:

Derive the formula for that velocity of satellite assuming the mass of the planet M and mass of satellite as m .

Text Solution

Verified by Experts

Critical velocity of a satellite revolving around the planet in circular orbit can be derived as follows: Consider the satellite of mass m revolving at height around the planet of mass M and radius above . As the satellite is moving in circular orbit, centripetal force acting on it is provided by the gravitational force of the planet,
i e . , `(mv^(2))/(r)=(GMm)/(r^(2))`
But r =R+h
`therefore" " v^(2)=(GM)/((R+h))`
`therefore" " v=sqrt((GM)/(R+h))`
Hence , critical velocity is given by formula
`sqrt((GM)/(R+h))`.
Promotional Banner

Topper's Solved these Questions

  • SPACE MISSIONS

    TARGET PUBLICATION|Exercise Practice Problems|4 Videos

  • SPACE MISSIONS

    TARGET PUBLICATION|Exercise Apply your Knowledge|2 Videos

  • SPACE MISSIONS

    TARGET PUBLICATION|Exercise Complete the given Chart/table|1 Videos

  • SOCIAL HEALTH

    TARGET PUBLICATION|Exercise CHAPTER ASSESSMENT|3 Videos

  • TOWARDS GREEN ENERGY

    TARGET PUBLICATION|Exercise Chapter Assessment|2 Videos

Similar Questions

Explore conceptually related problems

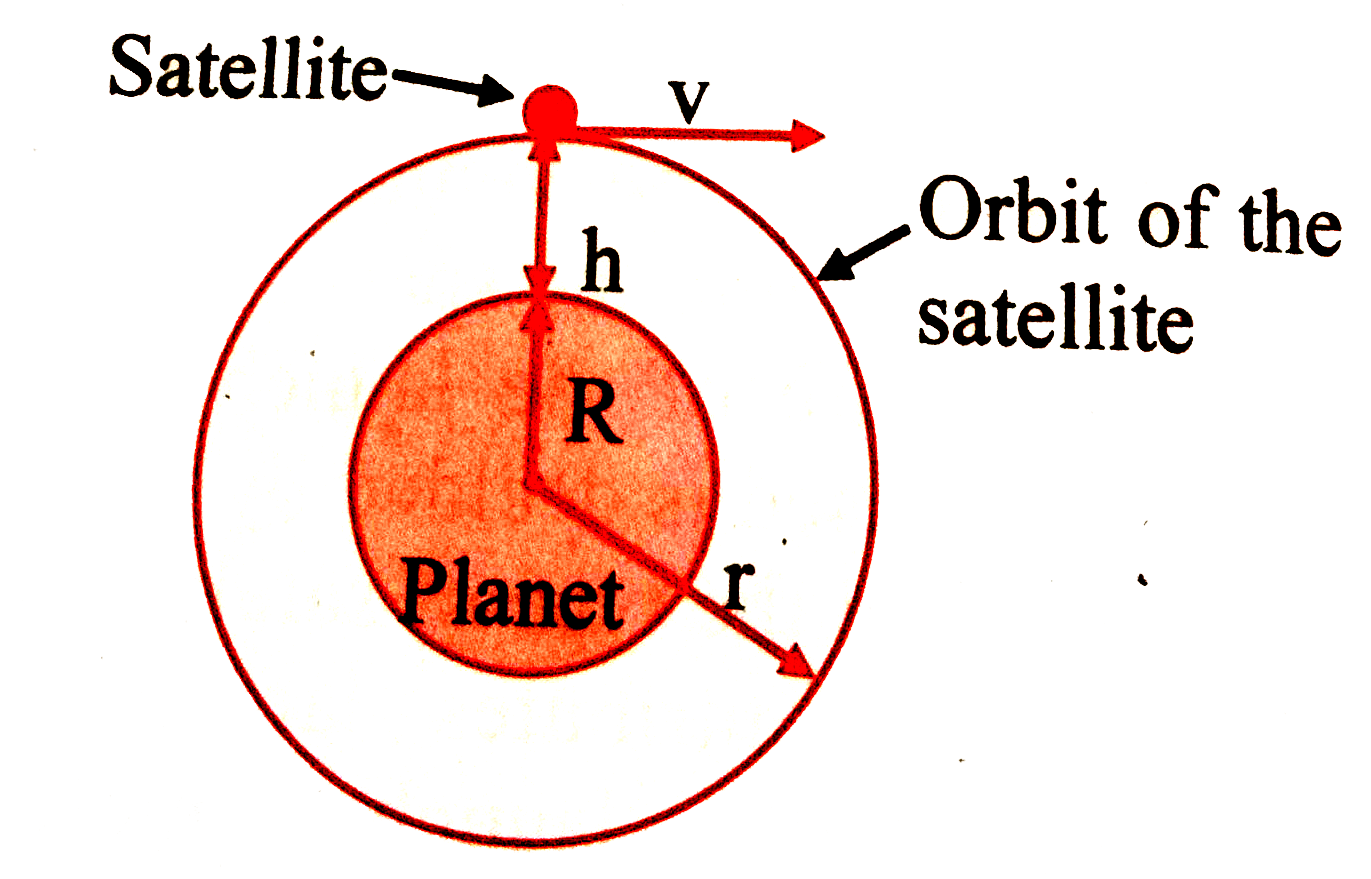
Observe the following diagram and answer the questions: on which factors does the velocity of the satellite depend ?

Observe the following diagram and answer the questions: What all factors are decided depending on the functions of a satellite ?

Observe the following diagram and answer the questions How will the value of F change if the mass m_2 is incresed to 4m_2 ?

How does the orbital velocity of a satellite depend on the mass of the satellite ?

Orbital velocity of a satellite depends on the ………..the planet around which the satellite revolves.

If r represents the radius of the orbit of a satellite of mass m moving around a planet of mass M , the velocity of the satellite is given by

The escape velocity of a satellite from the surface of a planet is sqrt(2) times the orbital velocity of the satellite. If the ratio of the masses of two given planets is 1 : 4 and that of their radii is 1 : 2, respectively, then find the ratio of escape velocities of a satellite from the surfaces of two planets.

Define orbital velocity. Derive an expression for the orbital velocity of a satellite revolving around a planet

Why the motion of a satellite around a planet cannot be taken as S.H.M ?

Why the motion of a satellite around a planet cannot be taken as S.H.M ?