Topper's Solved these Questions
PYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE ( 3 MARK QUESTIONS )|8 VideosPYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE ( 2 MARK QUESTIONS )|2 VideosPYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE ( 1 MARK MULTIPLE CHOICE QUESTIONS )|11 VideosPROBABILITY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNEMENT 5.4|12 VideosQUADRATIC EQUATION
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise CHALLENGIN QUESTIONS|2 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-PYTHAGORAS THEOREM-EXAMPLES FOR PRACTICE (2 MARK QUESTIONS )
- In right angled triangle , the lengtj of the perpendicular sides ar...
Text Solution
|
- If the sides of the triangle are 12, 35 and 37 , determine whether t...
Text Solution
|
- 10 m लंबी एक सीढी एक दीवार पर टिकाने पर भूमि से 8 m की उँचाई पर स्थित ...
Text Solution
|
- Determine whether (11,12,15) is a Pythagorean triplet ? Justify .
Text Solution
|
- Find the side of a square whose diagonal is 16sqrt(2)cm.
Text Solution
|
- Find the perimeter of an isosceles right angled triangle with each ...
Text Solution
|
- Complete the following activity to find the length of median AQ on sid...
Text Solution
|
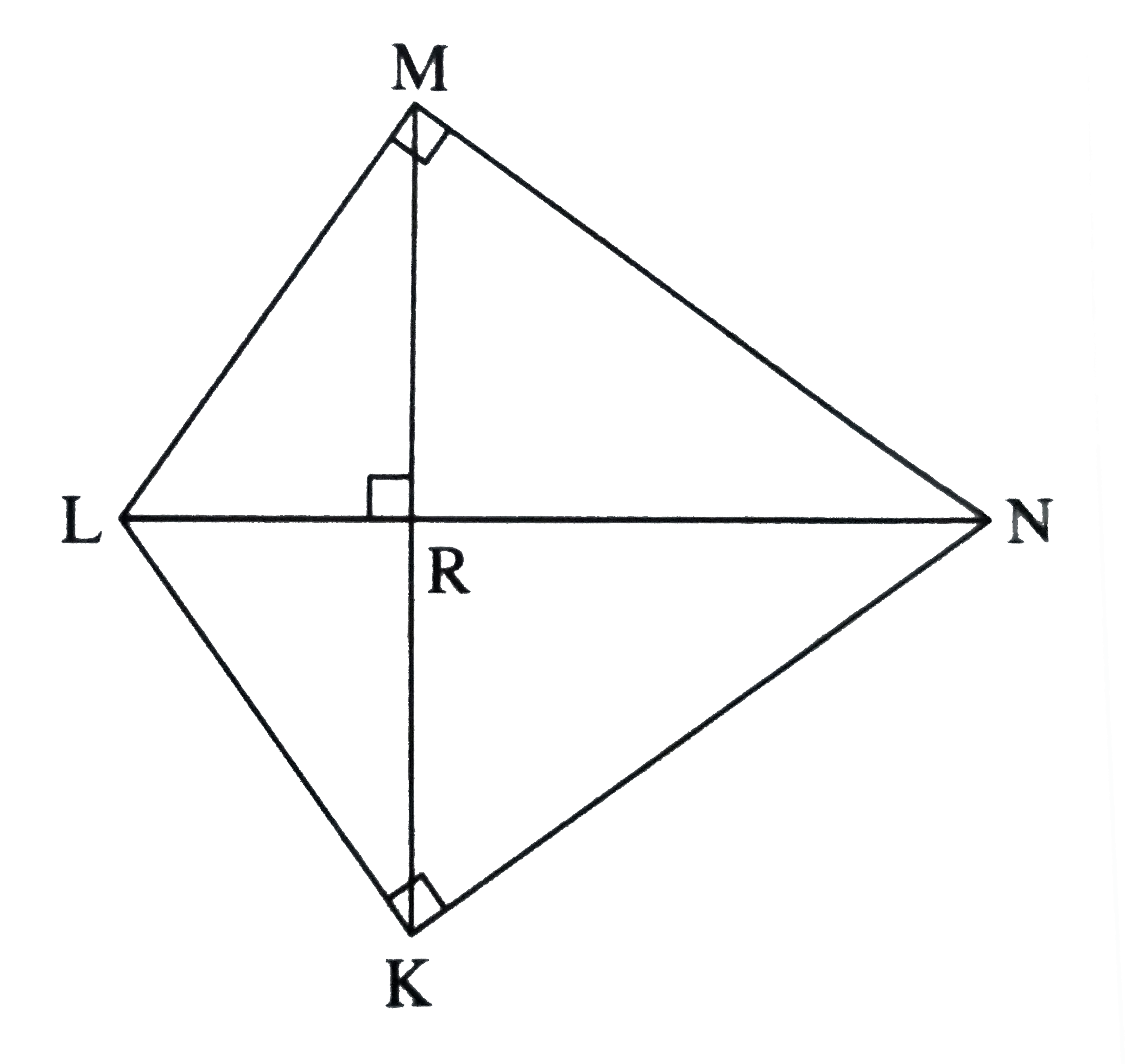
- In the figure , angle LMN = angle LKN = 90^(@) seg MK bot seg LN...
Text Solution
|
- In right angled DeltaABC, BDbotAC. If AD=4, DC=9, then find BD.
Text Solution
|