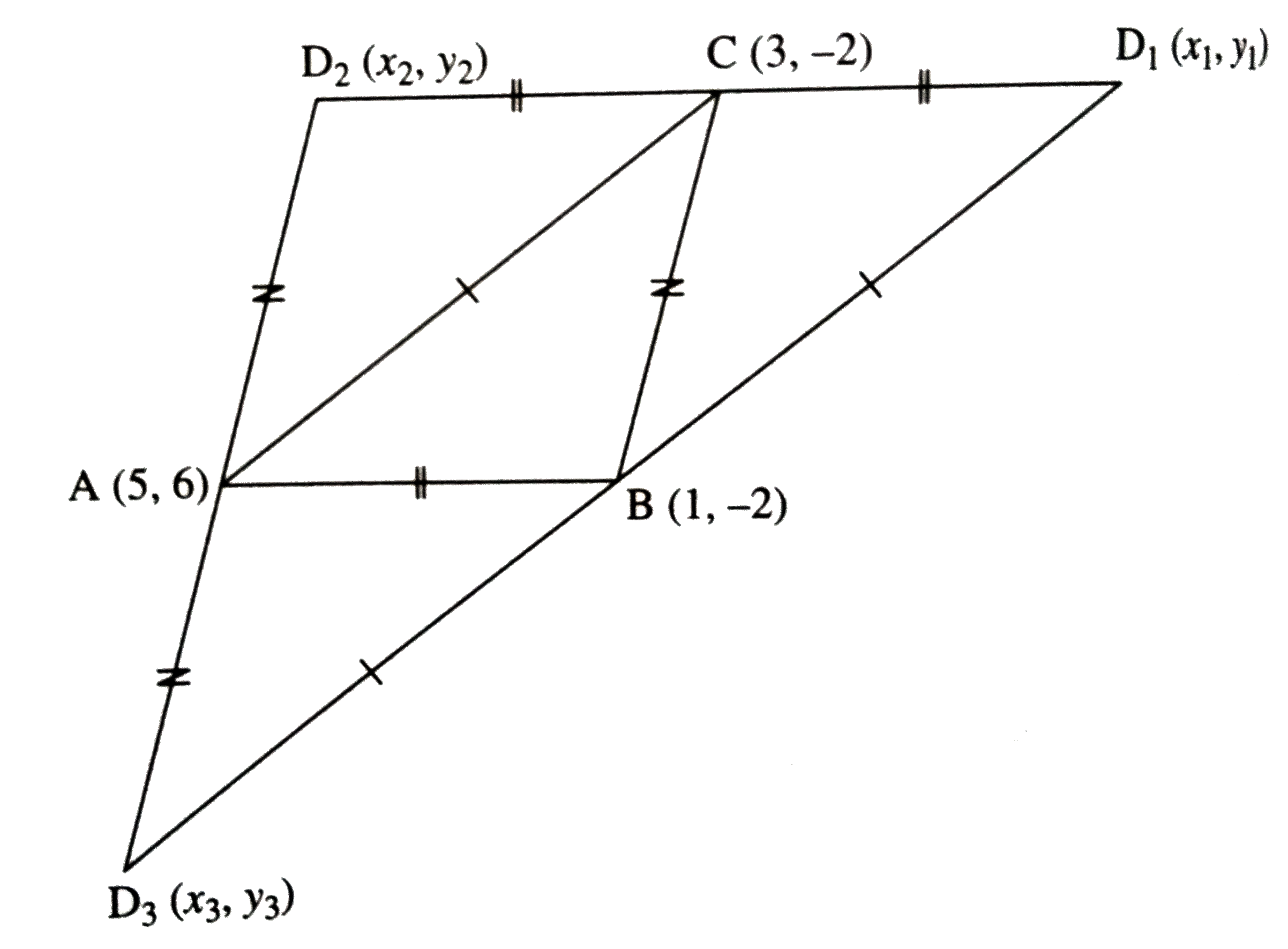
`A(5,6),B(1,-2)` and `C(3,-2)` are the vertices of a parallelogram.
There can be three possibilities of the location of the vertex D, say `D_(1)(x_(1),y_(2)),D_(2)(x_(2),y_(2))` and `D_(3)(x_(3),y_(3))` as shown in the figure.
`squareABD_(1)C` is a parallelogram.
`:.AB=CD_(1)`
......(Opposite sides of parallelogram are equal ) .........1
also `squareABCD_(2)` is parallelogram.
`:.AB=CD_(2)`
.........(Opposite sides of parallelogram are equal) ..........2
`:.` From 1 and 2
`CD_(1)=CD_(2)`
`:.C` is the midpoint of `D_(2)D_(1)`.
Similarly B is the midpoint of `D_(1)D_(3)`
and A is the midpoint of `D_(2)D_(3)`
Now C is the midpoint of `D_(2)D_(1)`
`:.` by midpoint formula
`3=(x_(2)+x_(1))/2`
`:.x_(1)+x_(2)=6` .............3
Similarly `x_(2)+x_(3)=10`.......4
and `x_(1)+x_(3)=2`.........5
Adding 3, 4 and 5 we get
`x_(1)+x_(2)+x_(2)+x_(3)+x_(1)+x_(3)=6+10+2`
`:.2x_(1)+2x_(2)+2x_(3)=18`
`:.2(x_(1)+x_(2)+x_(3))=18`
`:.x_(1)+x_(2)+x_(3)=18/2`
`:.x_(1)+x_(2)+x_(3)=9`.....6
Substituting 3 in 6 we get
`6+x_(3)=9`
`:.x_(3)=9-6`
`:.x_(3)=3`
Substituting 4 in 6 we get
`x_(1)+10=9`
`:.x_(1)=9-10`
`:.x_(1)=-1`
Substituting 5 in 6 we get
`x_(2)+2=9`
`:.x_(2)=9-2`
`:.x_(2)=7`
`:.x_(2)=7`
C is the midpoint of `D_(2)D_(1)`.
`:.` by midpoint formula,
`-2=(y_(1)+y_(2))/2`
`:.y_(1)+y_(2)=-4`..7
Similarly `y_(2)+y_(3)=12`............8
and `y_(1)+y_(3)=-4`.....9
Adding 7, 8 and 9 we get
`y_(1)+y_(2)+y_(2)+y_(3)+y_(1)+y_(3)=-4+12-4`
`:.2y_(1)+2y_(2)+2y_(3)=4`
`:.2(y_(1)+y_(2)+y_(3))=4`
`:.y_(1)+y_(2)+y_(3)=4/2`
` :.y_(1)+y_(2)+y_(3)=2`.....10
Substituting 7 in 10 we get
`-4+y_(3)=2`
`:.y_(3)=2+4`
`:.y_(3)=6`
Substiting 8 in 10 we get
`y_(1)+12=2`
`:.y_(1)=2-12`
`:.y_(1)=-10`
Substituting 9 and 10 we get
`y_(2)+(-4)=2`
`:.y_(2)-4=2`
`:.y_(2)=2+4`
`:.y_(2)=6`
The coordinates of point `D_(1)` are `(-1,10)`
The coordinates of point `D_(2)` are (7,6).
The coordinates of point `D_(3)` are (3,6).
The possible pairs of coordinates of the fourth vertex D of the parallelogram are `(-1,-10),(7,6)` and `(3,6)`.
