Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVIATION
PRADEEP|Exercise VALUE BASED QUESTIONS|5 VideosGRAVIATION
PRADEEP|Exercise CURIOSITY QUESTION|1 VideosGRAVIATION
PRADEEP|Exercise VERY SHORT ANSWER QUESTIONS|11 VideosBEHAVIOUR OF PERFECT GAS & KINETIC THEORY
PRADEEP|Exercise Assertion - Reason Type questions|14 VideosKINEMATICS
PRADEEP|Exercise 1 NCERT Comprehension|4 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-GRAVIATION-QUESTIONS
- A mass m is at a distance a from one end of a uniform rod of length l ...
Text Solution
|
- If the radius of the earth decreases by 1% without changing its mass, ...
Text Solution
|
- A missile is fired radially from the surface of earth (radius 6.4 xx 1...
Text Solution
|
- At noon, the sun and the earth pull the objects on the earth's surface...
Text Solution
|
- The largest and the shorest distance of earth from the sun 1.1 AU and ...
Text Solution
|
- Explain the use of multistage rockets in launching a satellite.
Text Solution
|
- Assertion: A person sitting in an artificial satellite revolving aroun...
Text Solution
|
- Can a satellite move in a stable orbit in a plane not passing through ...
Text Solution
|
- Among the known types of forces in nature, the gravitational force is ...
Text Solution
|
- All planets are spherical, why are they not cubical or cylindrical?
Text Solution
|
- A mass m is at a distance a from one end of a uniform rod of length l ...
Text Solution
|
- A solid sphere of uniform density and radius R applies a gravitational...
Text Solution
|
- Three solid spheres each of mass m and radius R are released from the ...
Text Solution
|
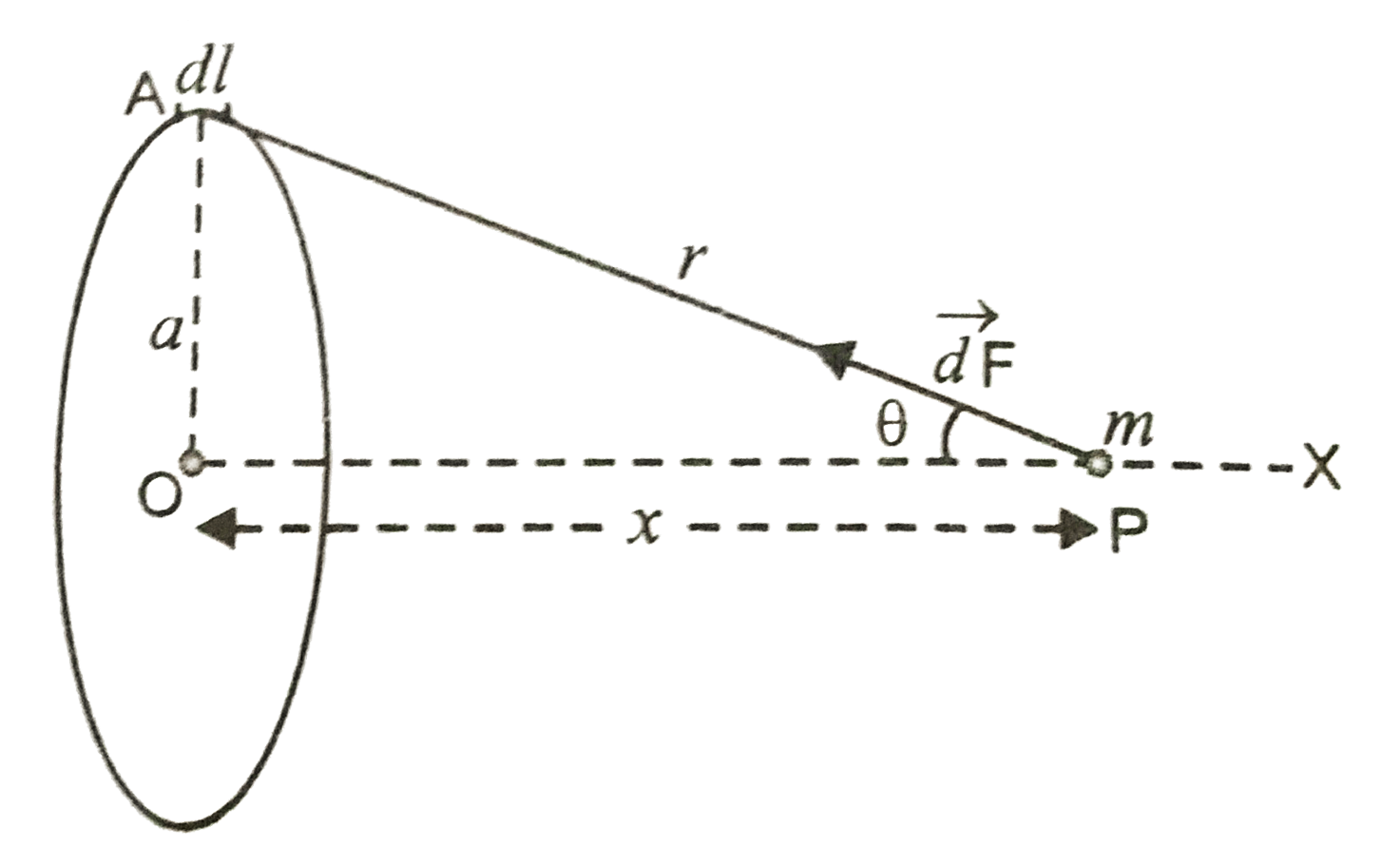
- Find the intensity of gravitational field at a point lying at a distan...
Text Solution
|