A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
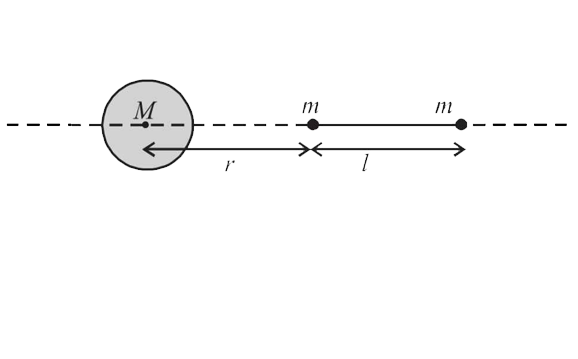
- A larger spherical mass M is fixed at one position and two identical p...
Text Solution
|
- A larger spherical mass M is fixed at one position and two identical p...
Text Solution
|
- Find the potential energy of the gravitational interaction of a point ...
Text Solution
|
- Find the potential energy of the gravitational interation of a point m...
Text Solution
|
- Two identical unifrom rods OA and OB each of length l and mass m are c...
Text Solution
|
- Two identical unifrom rods OA and OB each of length l and mass m are c...
Text Solution
|
- Two identical unifrom rods OA and OB each of length l and mass m are c...
Text Solution
|
- Figure shows two uniform rods of mass M and length l placed on two per...
Text Solution
|
- एक बड़ा गोलाकार द्रव्यमान M एक जगह स्थित है तथा दो एकरूप बिन्दु द्रव्यम...
Text Solution
|