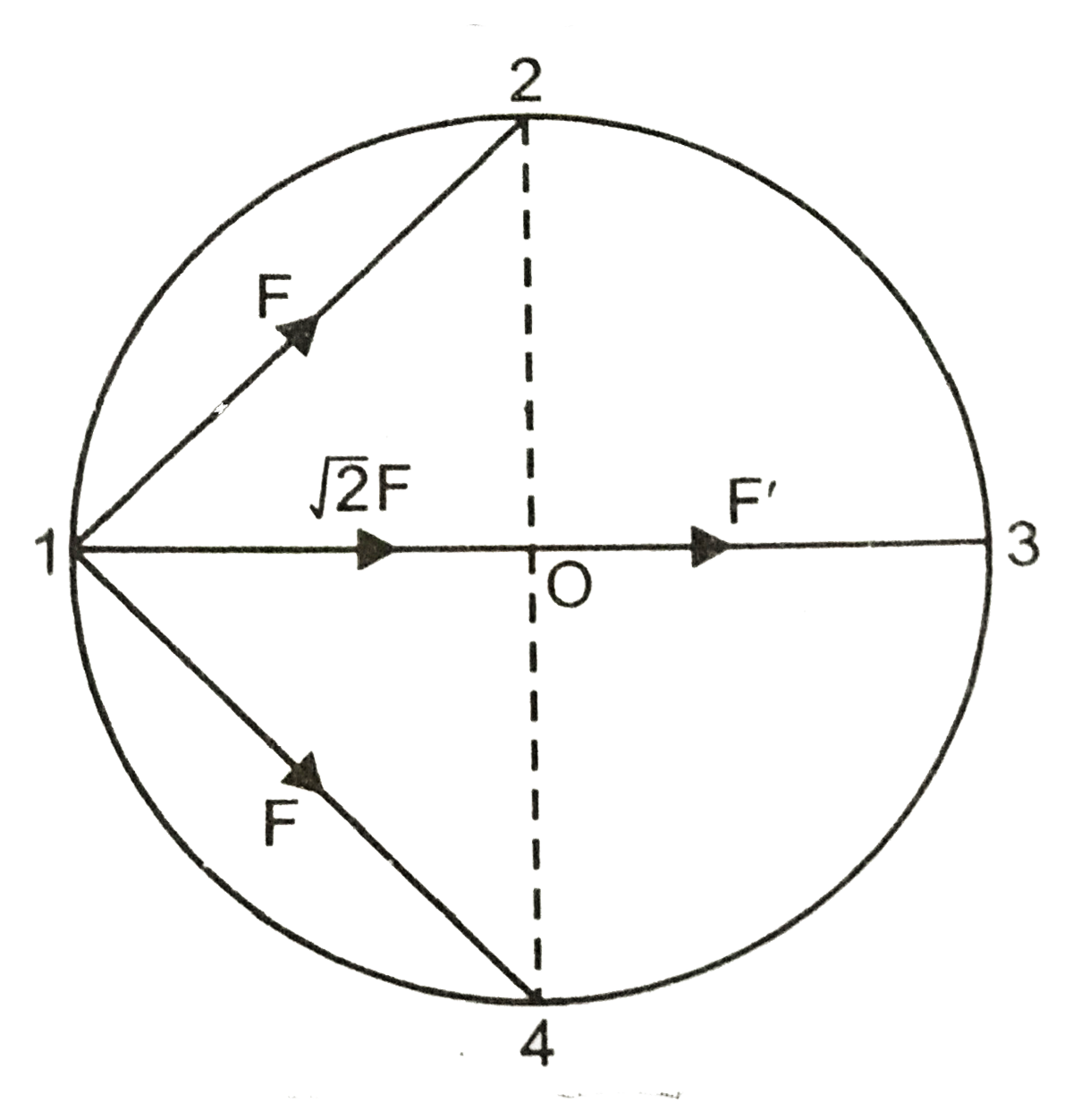
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- For particles of equal masses M that move along a circle of radius R u...
Text Solution
|
- For particles of equal massses M move along a circle of radius R under...
Text Solution
|
- Two particles of equal mass (m) each move in a circle of radius (r) un...
Text Solution
|
- Two particles each of equal mass (m) move along a circle of radius (r)...
Text Solution
|
- Two particles of equal mass m go round a circle of radius R under the ...
Text Solution
|
- Two particles of equal mass m go round a circle of radius R under the ...
Text Solution
|
- Four particles of equal masses M move along a circle of radius R under...
Text Solution
|
- Two particles of equal mass move in a circle of radius r under the act...
Text Solution
|
- Two particles of equal mass move in a circle of radius r under the act...
Text Solution
|