Home
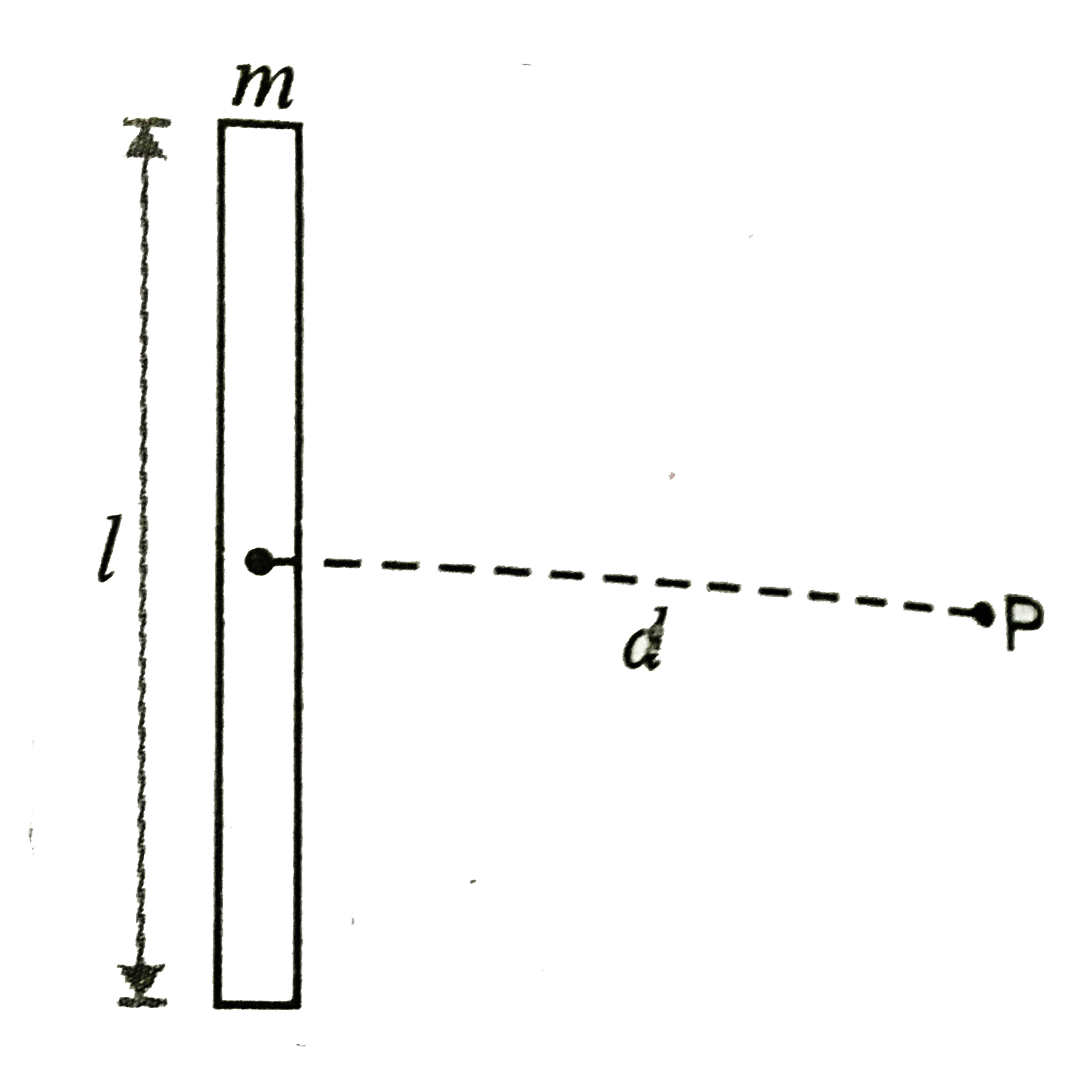
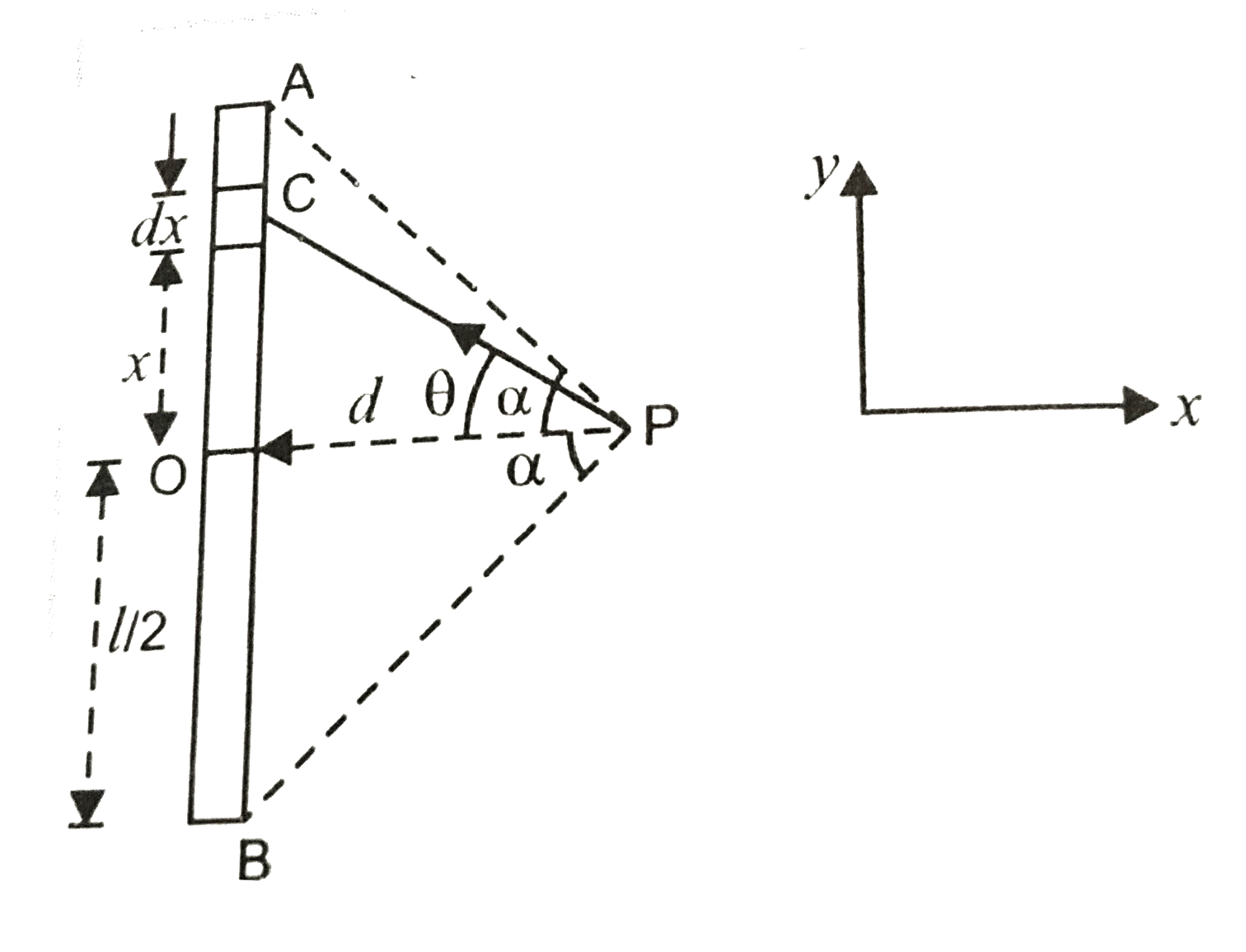
Class 11
PHYSICS
A uniform rod of mass m and length l is ...

A uniform rod of mass `m` and length `l` is taken. Find the gravitational field intensity at point `P` at distance `d` which is on the perpendicular bisector of the rod as shown in Fig.

A

`(4Gm)/(d sqrt(4d^(2) + l^(2)))`

B

`(2Gm)/(d sqrt(l^(2)+ 4d^(2)))`

C

`(2sqrt(2)Gm)/(d sqrt(l^(2)+ 4d^(2)))`

D

none of the above

Text Solution

Verified by Experts

The correct Answer is:
B
Consider element of the rod of width `x` as shown in Fig.

Mass of element, `dm = (m)/(l) dx`
Gravitaitonal field intensity at `P` due to this element is
`dI = (Gdm)/(x^(2) + d^(2)) = (G)/((x^(2) + d^(2))) xx (m)/(l) dx` along `PC`
In `deltaOPC, x = d tan theta` and `dx = d sec^(2) theta d theta`
`:.x^(2) + d^(2) = d^(2) (tan^(2) theta + 1) = d^(2) sec^(2) theta`
`:. dI = (Gm)/(l) (d sec^(2) theta d theta)/(d^(2) sec^(2) theta) = (Gm)/(ld) d theta`
resolving `d vecI` into two rectangular components we have `dI cos theta` acts along `PO` and `dI sin theta` acts perpendicular to `PO`.
If we find the gravitaitonal field due to other elements of the rod at `P` and resolve them into two rectangular componets, we note that the components of gravitational field intensity perpendicular to `OP` will cancel out and components of gravitational intensity along `PO` will be added up. Therefore, total gravitational intensity at `P` due to entire rod is
`I = int_(-alpha)^(+alpha) dI cos theta = int_(-alpha)^(+alpha) (Gm)/(ld) cos theta d theta`
`= (Gm)/(ld) [2sin alpha] = (2Gm)/(ld) xx (l//2)/(sqrt((l//2)^(2) + d^(2)))`
`= (2Gm)/(dsqrt(l^(2) + 4d^(2)))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance of (L )/(4 ) from centre and perpendicular to rod.

A uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v_(0) perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.

A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B , perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance (l)/(6) from the centre towards A of the rod after time t = (pi m l)/(12 J) is.

A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:

The radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l/4 from its one end will be

A uniform rod of mass m and length L is fixed to an axis, making an angle theta with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?

A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a/4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.

A uniform rod of mass M and length L carrying a charge q uniformly distributed over its length is rotated with constant velocity w about its mid point perpendicular to the rod. Its magnetic moment is

A uniform rod of mass M and length l is hinged at point O and is free to rotate on a horizontal smooth surface. Point O is at a distance of (l)/(4) from one end of the rod. A sharp impulse P_(0) = 2 sqrt(130) kg m//s is applied along the surface at one end of the rod as shown in figure [tan theta = (9)/(7)] (a) Find the angular speed of the rod immediately after the hit (b) Find the impulse on the rod due to the hinge.

A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is