A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
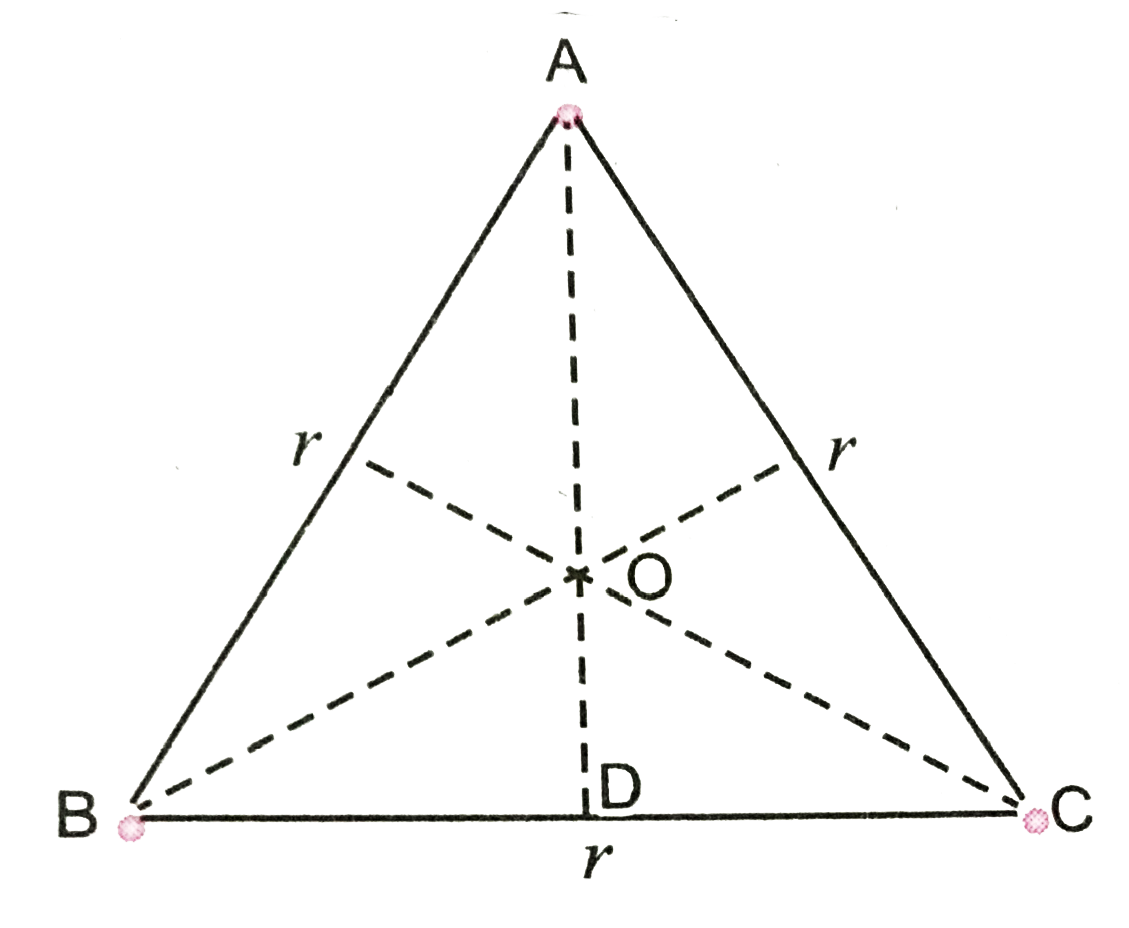
- There are three identical point mass bodies each of mass m locted at t...
Text Solution
|
- Three point masses 'm' each are placed at the three vertices of an equ...
Text Solution
|
- There are three identical point mass bodies each of mass m locted at t...
Text Solution
|
- There are three identical point mass bodies each of mass m locted at t...
Text Solution
|
- There are three identical point mass bodies each of mass m locted at t...
Text Solution
|
- There are three identical point mass bodies each of mass m locted at t...
Text Solution
|
- Three point masses each of mass m rotate in a circle of radius r with ...
Text Solution
|
- Three mass points each of mass m are placed at the vertices of an equi...
Text Solution
|
- Three particles each of mass m are kept at vertices of an equilateral ...
Text Solution
|