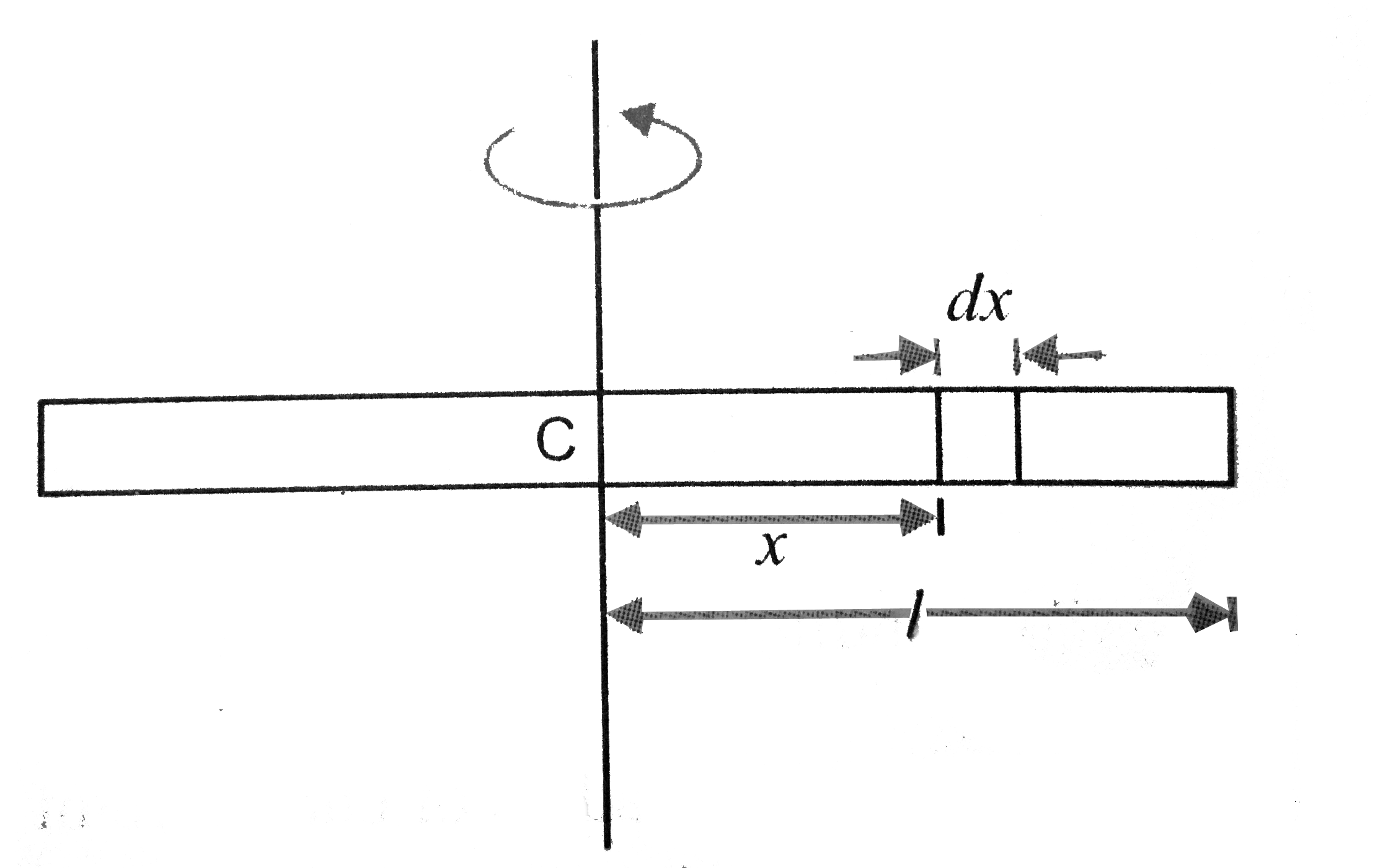
Text Solution
Verified by Experts
Recommended Questions
- A steel rod of length 2l cross-sectional area A and mass M is set rota...
Text Solution
|
- The radius of gyration of an uniform rod of length L about an axis pas...
Text Solution
|
- A uniform rod of length l, mass m, cross-sectional area A and Young's ...
Text Solution
|
- A steel rod of length 2l cross-sectional area A and mass M is set rota...
Text Solution
|
- A rod PQ of length L revolves in a horizontal plane about the axis YY´...
Text Solution
|
- A uniform rod of mass m. length L, area of cross- secticn A is rotated...
Text Solution
|
- A thin uniform copper rod of length l and cross-section area A and mas...
Text Solution
|
- A uniform rod of mass m and length l is rotating with constant angular...
Text Solution
|
- A thin uniform rod of mass M and length L is rotating about a perpendi...
Text Solution
|