Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
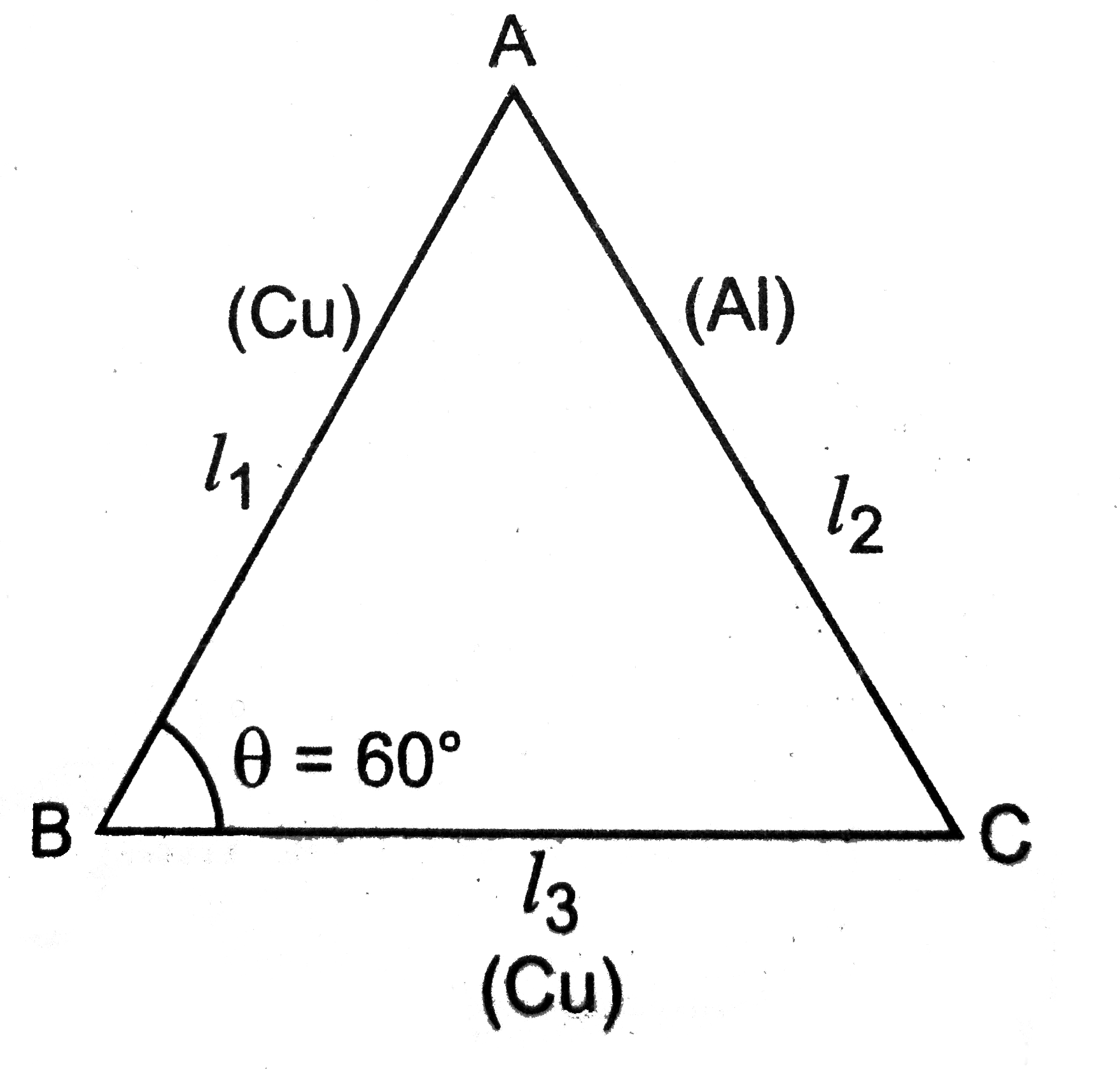
- An equilateral triangle ABC if formed by two Cu rods AB and BC and one...
Text Solution
|
- An equilateral triangle ABC if formed by two Cu rods AB and BC and one...
Text Solution
|
- The moment of inertia of a rod about its perpendicular bisector is I ....
Text Solution
|
- Three rods of equal lengths are joined to form an equilateral triangle...
Text Solution
|
- There are two rods of length l1 l2 and coefficient of linear expansion...
Text Solution
|
- As shown in the figure , an equilateral triangle ABC is formed by join...
Text Solution
|
- Three rods of equal length at 0^(@)C, are connected with one another t...
Text Solution
|
- Among three rods, the first two are made of same material having coeff...
Text Solution
|
- एक समबाहु त्रिभुज ABC दो Cu की छड़ों AB व BC एवं एक Al की छड़ द्वारा ब...
Text Solution
|