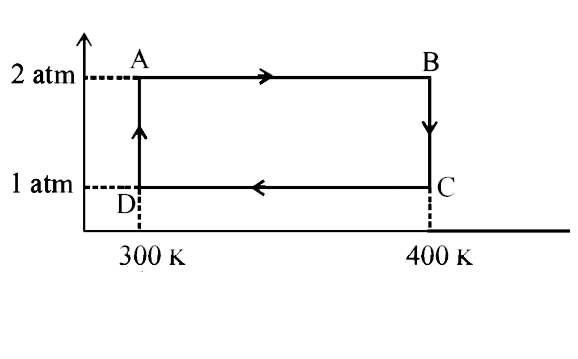
Text Solution
Verified by Experts
Topper's Solved these Questions
THERMODYNAMICS
PRADEEP|Exercise Value based Questions|4 VideosTHERMODYNAMICS
PRADEEP|Exercise NCERT Questions|10 VideosTHERMODYNAMICS
PRADEEP|Exercise Long answer questions(NCERT)|5 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise Assertion- Reason Type questions|20 VideosWORK, ENERGY AND POWER
PRADEEP|Exercise Assertion-Reason Type Questions|24 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-THERMODYNAMICS-Higher order thinking skills
- (Figure) Shows three isothermal curves at temp T(1), T(2) and T(3) T...
Text Solution
|
- A sample of 2 kg of monoatomic helium (assumed ideal) is taken through...
Text Solution
|
- Figure. Shows an ideal gas changing its state A to state C by two diff...
Text Solution
|
- Two moles of helium gas undergo a cyclic process as shown in Fig. Assu...
Text Solution
|
- A thermos flask contains coffee. It is shaken vigorously. (i) Has any ...
Text Solution
|
- At 27^@C two moles of an ideal monatomic gas occupy a volume V. The ga...
Text Solution
|
- A sample of an ideal gas is taken through the cyclic process abca . It...
Text Solution
|
- The initial volume of an ideal gas is V(1) and the initial pressure is...
Text Solution
|
- About 0.014 kg nitrogen is enclosed in a vessel at temperature of 27^...
Text Solution
|