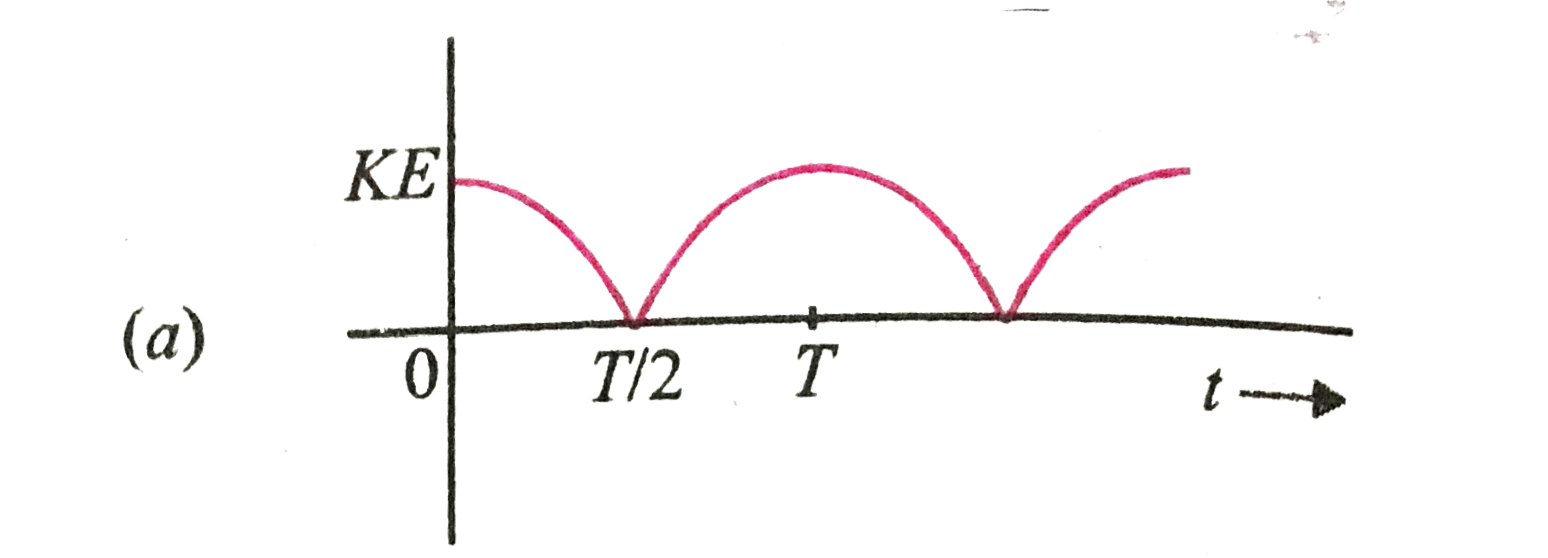
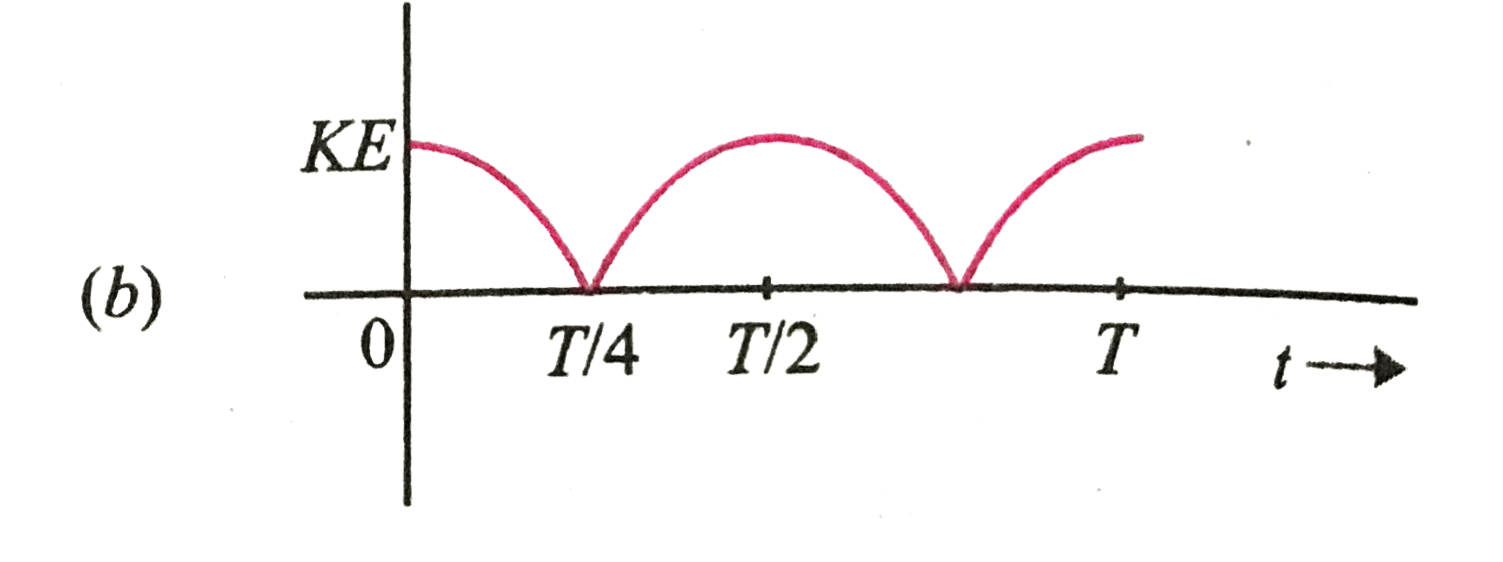
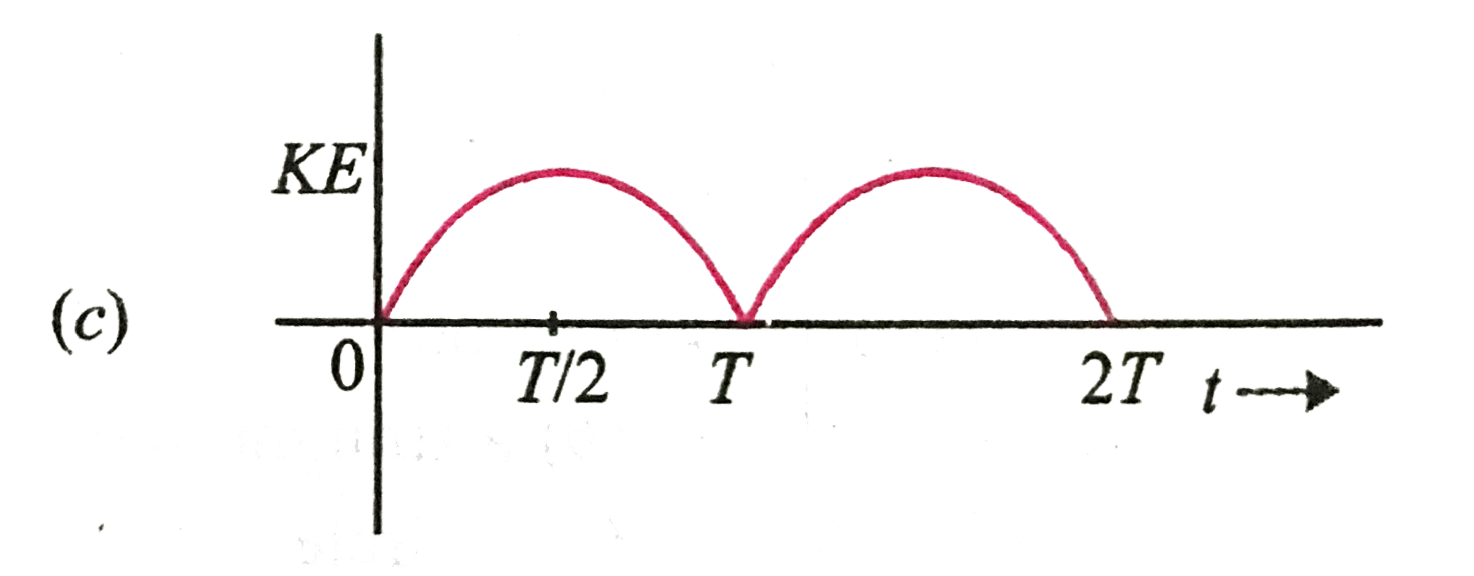
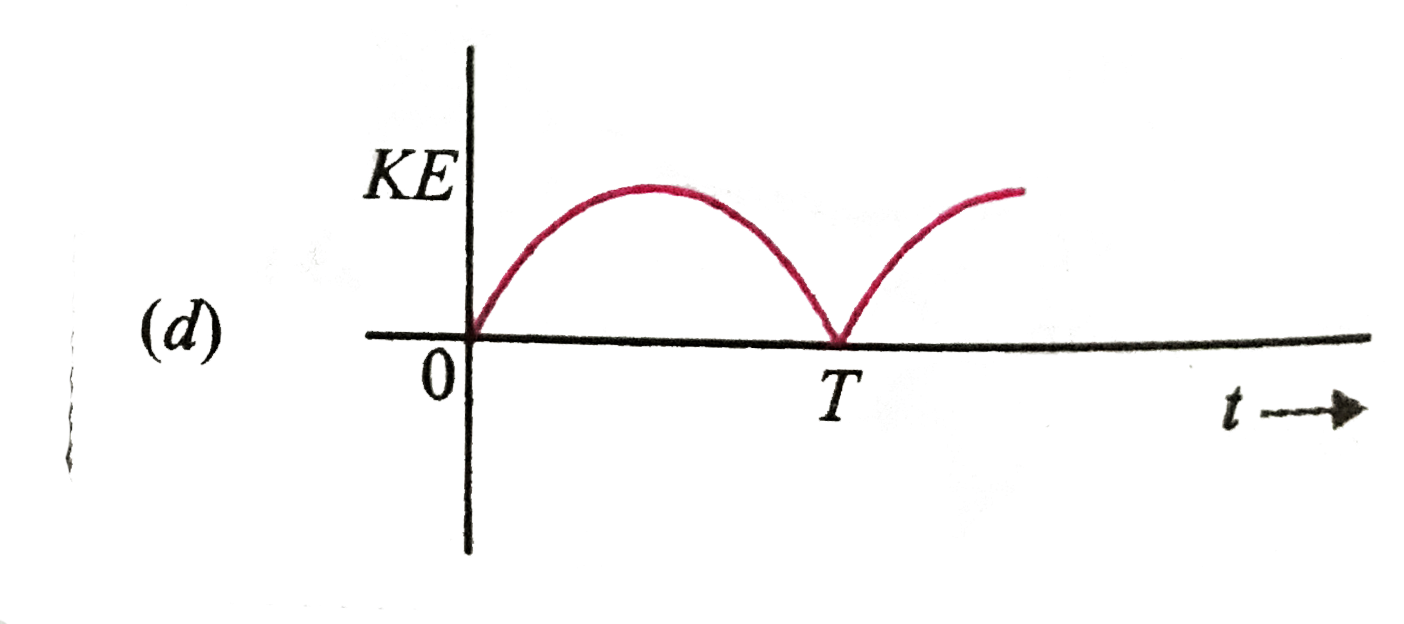
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS AND WAVES
PRADEEP|Exercise integer type question|8 VideosOSCILLATIONS AND WAVES
PRADEEP|Exercise Assertion-Reason Type Questions|23 VideosOSCILLATIONS AND WAVES
PRADEEP|Exercise Multiple Choice Question-II|14 VideosMATHEMATICAL TOOLS
PRADEEP|Exercise Fill in the blanks|5 VideosPHYSICAL WORLD AND MEASUREMENT
PRADEEP|Exercise Competiton Focus Jee Medical Entrance|18 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-OSCILLATIONS AND WAVES-JEE mains adv..(multiple choice quection)
- A point mass is subjected to two simultaneous sinusoidal displacements...
Text Solution
|
- Out of the following function reporesenting motion of a particle which...
Text Solution
|
- A particle is executing simple harmonic motion with a time period T. A...
Text Solution
|
- A body is executing simple harmonic motion. At a displacement x its po...
Text Solution
|
- For a simple pendulum, a graph is plotted its kinetic energy (KE) and ...
Text Solution
|
- A solid cube of side a and density rho(0) floats on the surface of a l...
Text Solution
|
- A pendulum bob has a speed 3m/s while passing thorugh its lowest posit...
Text Solution
|
- A uniform cylinder of length (L) and mass (M) having cross sectional a...
Text Solution
|
- An ideal gas enclosed in a cylindrical container supports a freely mov...
Text Solution
|
- A simple pendulum is oscillating without damiping, When the displaceme...
Text Solution
|
- There is a rod of length l and mass m. It is hinged at one end to the ...
Text Solution
|
- Two simple pendulums have time period T and 5T//4. They start vibratin...
Text Solution
|
- A simple pendulum has time period (T1). The point of suspension is now...
Text Solution
|
- A simple pendulum of length L is suspended from the top of a flat bea...
Text Solution
|
- A pendulum suspended from the roof of an elevator at rest has a time ...
Text Solution
|
- A spring of force constant k is cut into lengths of ratio 1 : 2 : 3. T...
Text Solution
|
- Three springs are connected to a mass m as shown in figure, When mas...
Text Solution
|
- A force of 6.4N streches a vertical spring by 0.1m The mass that must ...
Text Solution
|
- A body of mass m falls from a height h on to the pan of a spring balan...
Text Solution
|
- A block of mass m, attached to a spring of spring constant k, oscillte...
Text Solution
|