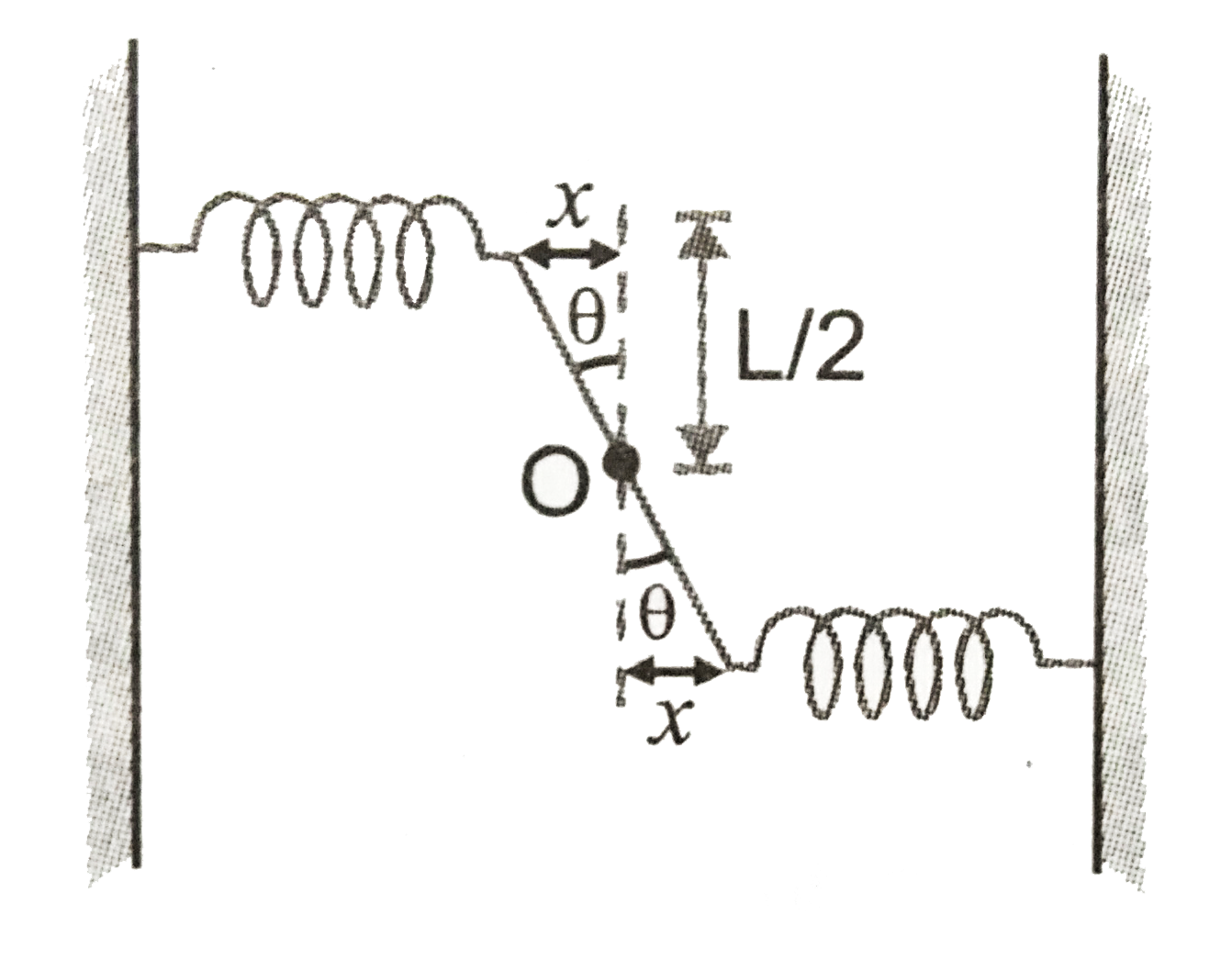
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS AND WAVES
PRADEEP|Exercise integer type question|8 VideosOSCILLATIONS AND WAVES
PRADEEP|Exercise Assertion-Reason Type Questions|23 VideosOSCILLATIONS AND WAVES
PRADEEP|Exercise Multiple Choice Question-II|14 VideosMATHEMATICAL TOOLS
PRADEEP|Exercise Fill in the blanks|5 VideosPHYSICAL WORLD AND MEASUREMENT
PRADEEP|Exercise Competiton Focus Jee Medical Entrance|18 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-OSCILLATIONS AND WAVES-JEE mains adv..(multiple choice quection)
- A block of weight W produces an extension of 9cm when it is hung by an...
Text Solution
|
- Two springs, of spring constants k(1) and K(2), have equal highest vel...
Text Solution
|
- A uniform rod of length (L) and mass (M) is pivoted at the centre. Its...
Text Solution
|
- The mass (M) shown in the figure oscillates in simple harmonic motion ...
Text Solution
|
- A particle of mass m is attached to three identical springs of spring...
Text Solution
|
- A wooden block performs SHM on a frictionless surface with frequency, ...
Text Solution
|
- A mass M attached to a horizontal spring executes SHM with an amplitud...
Text Solution
|
- If a spring of stiffness 'k' is cut into two parts 'A' and 'B' of leng...
Text Solution
|
- A particle, with restoring force proportional to displacement and resu...
Text Solution
|
- The amplitude of a damped oscillator decreases to 0/9 times ist oringi...
Text Solution
|
- If a simple pendulum has significant amplitude (up to a factor of1//e ...
Text Solution
|
- A wave in a string has an amplitude of 2 cm. The wave travels in the +...
Text Solution
|
- When a wave travels in a medium, th eparticle displacement is given by...
Text Solution
|
- 4.0 g of a gas occupies 22.4 litres at NTP. The specific heat capacity...
Text Solution
|
- If the intensity increased by a factor of 20, byhow may decibels is th...
Text Solution
|
- Four harmonic waves of equal freuencies and equal intensity I(0) have ...
Text Solution
|
- The amplitude of a wave disturbance propagating in the positive x-dire...
Text Solution
|
- If the equation of progressive wave is given by y=4 sin pi[(t)/(5)-(x)...
Text Solution
|
- A wave is represented by the equation y=(0.001mm)sin[(50s^-10t+(2.0m^-...
Text Solution
|
- In a sinusoidal wave the time required for a particular point to move ...
Text Solution
|
 .
.