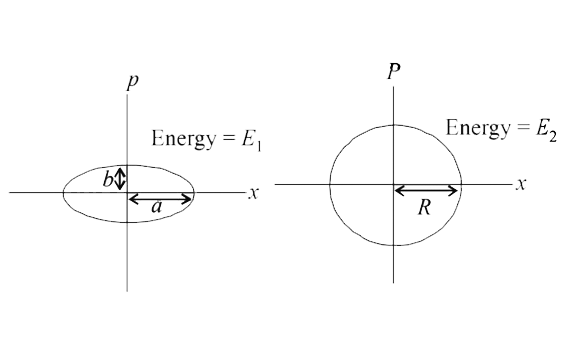
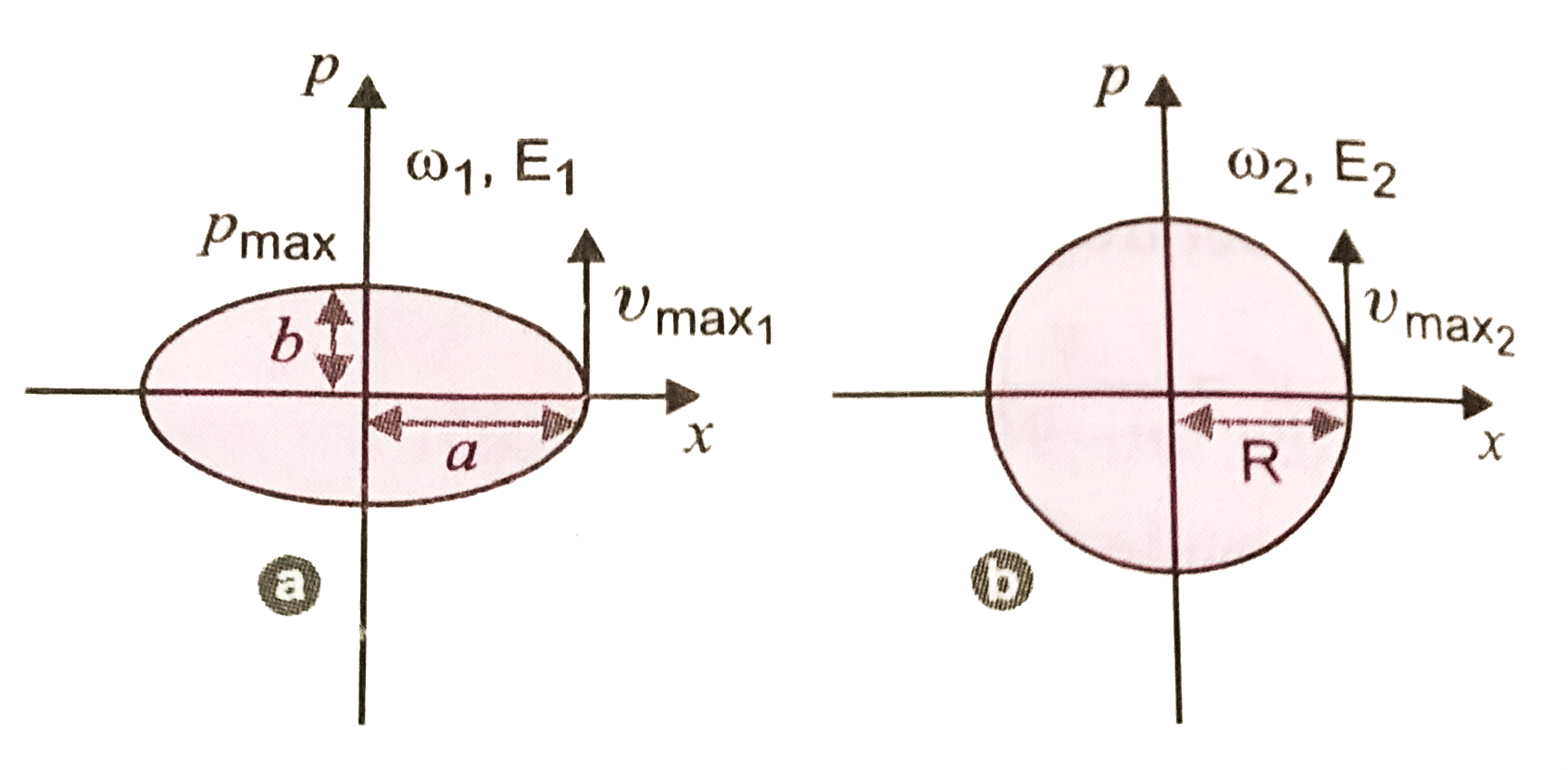
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS AND WAVES
PRADEEP|Exercise integer type question|8 VideosOSCILLATIONS AND WAVES
PRADEEP|Exercise Assertion-Reason Type Questions|23 VideosOSCILLATIONS AND WAVES
PRADEEP|Exercise Multiple Choice Question-II|14 VideosMATHEMATICAL TOOLS
PRADEEP|Exercise Fill in the blanks|5 VideosPHYSICAL WORLD AND MEASUREMENT
PRADEEP|Exercise Competiton Focus Jee Medical Entrance|18 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-OSCILLATIONS AND WAVES-JEE mains adv..(multiple choice quection)
- An observer is moving with half the speed of light towards a stationar...
Text Solution
|
- Two cars moving in opposite directio approach each other with speed of...
Text Solution
|
- Two independent harmonic oscillators of equal mass are oscillating abo...
Text Solution
|
- A mass m=100 gram is attached at the end of a light spring which osci...
Text Solution
|
- A linear harmonic oscillator of force constant 2 xx 10^6 N//m and ampl...
Text Solution
|
- For a particle executing S.H.M. which of the following statements hold...
Text Solution
|
- A block with mass (M) is connected by a massless spring with stiffness...
Text Solution
|
- If amplitude of a particle in S.H.M. is doubled, which of the followin...
Text Solution
|
- If a simple harmonic motion is given by y=(sin omegat+cosomegat)m ...
Text Solution
|
- If the different types of penulums are taken to moon, the time period ...
Text Solution
|
- Which of the following functions represents SHM
Text Solution
|
- Which of the following quantities are always zero in a S.H.M. ? Here, ...
Text Solution
|
- Which of the following statements are true for the ocsillations of the...
Text Solution
|
- Two particles A and B have a phase diference of pi when a sine wave pa...
Text Solution
|
- In a stationary wave
Text Solution
|
- A listener is at rest with respect to the source of sound. A wind star...
Text Solution
|
- The fundamental frequency of a vibrating organ pipe is 200Hz
Text Solution
|
- Function x=Asin^(2)omegat+Bcos^(2)omegat=Csinomegat cos omegat represe...
Text Solution
|
- Two blocks A and B, each of mass m, are connected by a masslesss sprin...
Text Solution
|
- When a body is suspended from two light springs separately, the period...
Text Solution
|