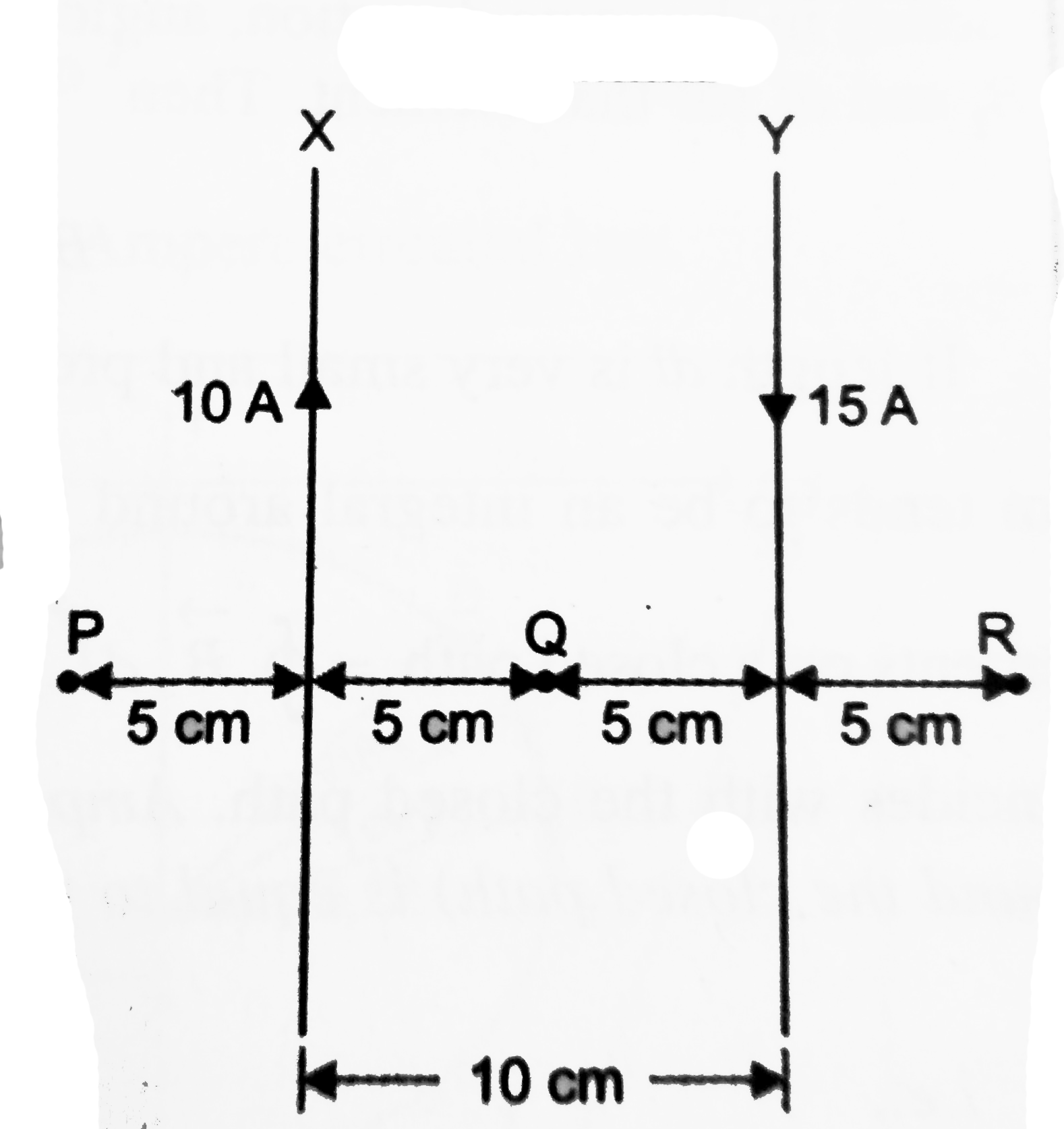
Text Solution
Verified by Experts
Topper's Solved these Questions
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
PRADEEP|Exercise Conceptual Problems (d)|2 VideosMAGNETIC EFFECT OF CURRENT AND MAGNETISM
PRADEEP|Exercise Very Short Answer Questions (a)|2 VideosELECTROSTATICS
PRADEEP|Exercise ASSERTION-REASON TYPE QUESTIONS|2 VideosOPTICS
PRADEEP|Exercise Multiple choice questions|1 Videos
Similar Questions
Explore conceptually related problems