Two wires A and B have the same length equal to `44cm`. and carry a current of `10A` each. Wire A is bent into a circle and wire B is bent into a square. (a) Obtain the magnitudes of the fields at the centres of the two wires. (b) Which wire produces a greater magnetic field at the centre?

Explanation

Here, `I=10A`,
length of each wire `=44cm`.
(a) Let r be the radius of the wire A when it is bent into a circle.
Then `2pir=44` or `r=(44)/(2pi)=7cm=7/100m`
Magnetic field induction at the centre of the circular coil carrying current is given by
`B=(mu_0)/(4pi)(2piI)/(r)=10^-7xx2xx22/7xx10xx100/7`
`=9*0xx10^-5T`
When another wire is bent into a square of each side L, then,
`4L=44` or `L=11cm=0.11m`

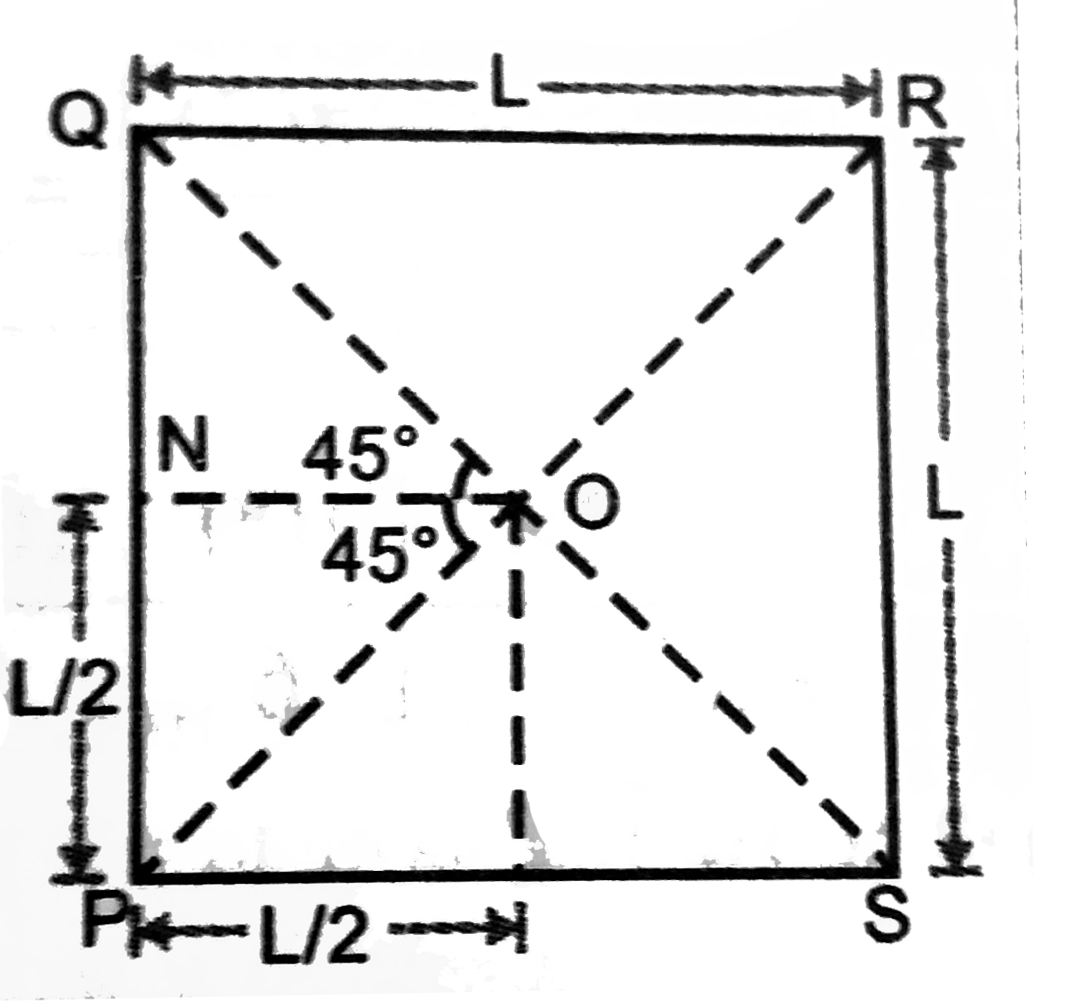
We know that magnetic field induction at a point, perpendicular distance a from the linear conductor carrying current I is given by,
`B=(mu_0)/(4pi)I/a(sin phi_1+sin phi_2)`
Here, `I=10A`, `a=L/2=11/2cm=11/200m`,
`phi_1=45^@` and `phi_2=45^@`
Since the centre O of the square is equidistant from the ends of each arm of the square and the current through each arm of the square contributes to the magnetic field in the same direction and of the same strength, hence, total magnetic field induction at point O is given by
`B=4xx(mu_0)/(4pi)I/a(sin 45^@+sin45^@)`
`=4xx10^-7xx(10)/((11//200))(1/sqrt2+1/sqrt2)`
`=10*3xx10^-5T`
(b) Thus, the magnetic field due to a square will be more than that due to a circle of same perimeter.