For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by `B=(mu_0IR^2N)/(2(x^2+R^2)^(3//2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel coaxial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R and is given by `B=0*72(mu_0NI)/(R)` approximately.
[Such as arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]

Explanation

(a) Given, `B=(mu_0IR^2N)/(2(x^2+R^2)^(3//2))`
When point is at the centre of circular coil, `x=0`.
Then, `B=(mu_0IR^2N)/(2R^3)=(mu_0IN)/(2R)`
Which is the same as the standard result.
(b) Here, `a=R`, `n=N`. Let d be the distance of point P from the mid-point O lying on the axis of the two circular coils C and D, where `dlt lt R`. In figure.

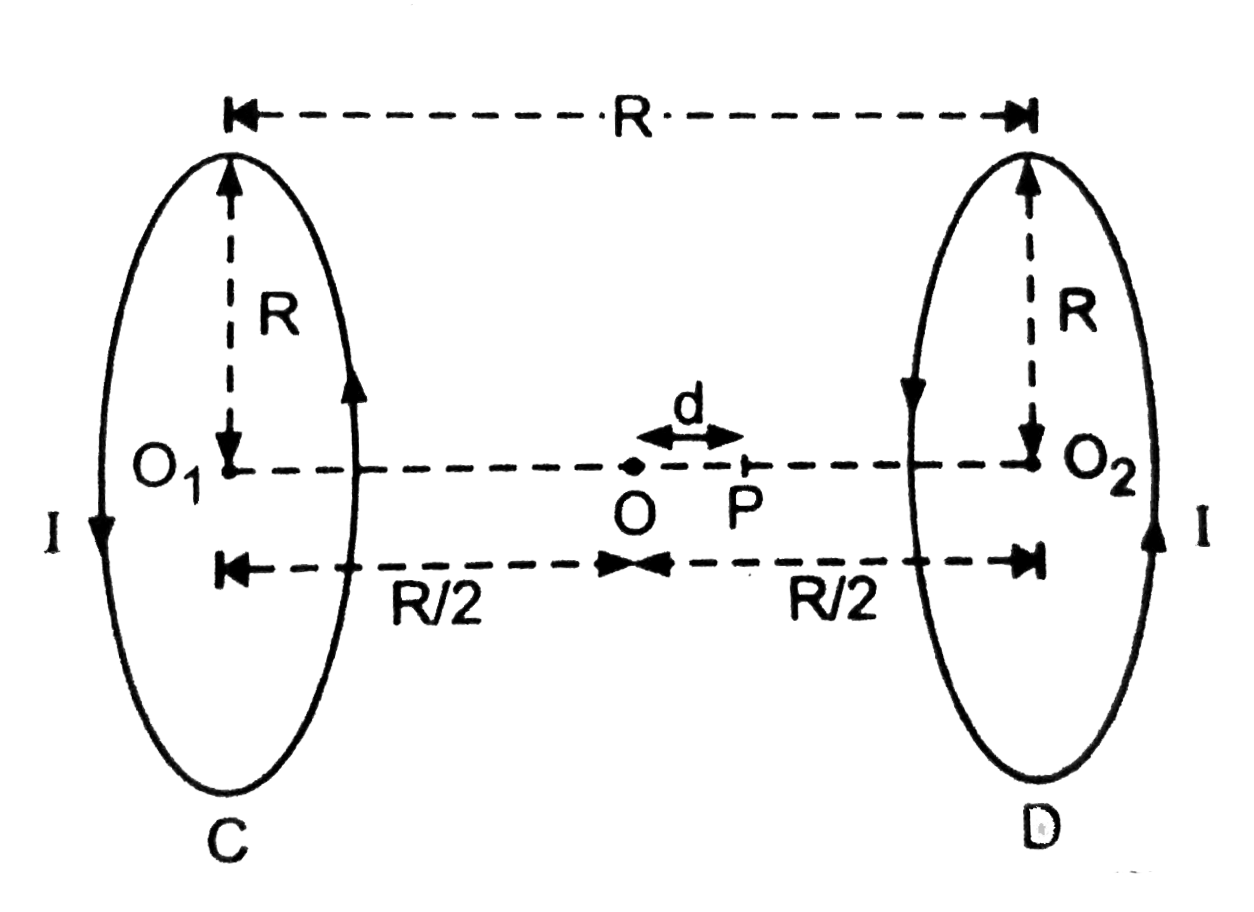
For coil C, `O_1P=x_1=R/2+d`
For coil D, `O_2P=x_2=R/2-d`
we know that magnetic field at a point on the axis of the circular coil of radius a, having n turns and carrying current I, which is at a distance x from the centre of the coil is given by
`B=(mu_0)/(4pi)(2pinIa^2)/((x^2+a^2)^(3//2))=(mu_0nIa^2)/(2(x^2+a^2)^(3//2))`
Due to coil C, magnetic field at P is
`B_1=(mu_0NIR^2)/(2(x_1^2+R^2)^(3//2))=(mu_0NIR^2)/(2[(R/2+d)^2+R^2]^(3//2))=(mu_0NIR^2)/(2)[(1)/((R^2/4+d^2+Rd+R^2)^(3//2))]`
As `d^2` can be neglected in comparison to `R^2`, therefore,
`B_1=(mu_0NIR^2)/(2)xx(1)/(((5R^2)/(4))^(3//2))[(1+(4d)/(5R))^(-3//2)]` It acts along `PO_2`.
Similarly, due to coil D, magnetic field at P is given by
`B_2=(mu_0NIR^2)/(2(x_2^2+R^2)^(3//2))=(mu_0NIR^2)/(2[(R/2-d)^2+R^2]^(3//2))=(mu_0NIR^2)/(2)xx(1)/(((5R^2)/(4))^(3//2))[(1-(4d)/(5R))^(-3//2)]`
It acts along `PO_2`.
Total magnetic field at P due to current through the coils is given by `B=B_1+B_2`
`=(mu_0NIR^2)/(2((5R^2)/(4))^(3//2))xx[(1+(4d)/(5R))^(-3//2)+(1-(4d)/(5R))^(-3//2)]=(mu_0NIR^2)/(2R^3)(4/5)^(3//2)[1-(6d)/(5R)+1+(6d)/(5R)]`
(From Binomial Theorem)
`=(4/5)^(3//2)(mu_0NI)/(R)=0*72(mu_0NI)/(R)`