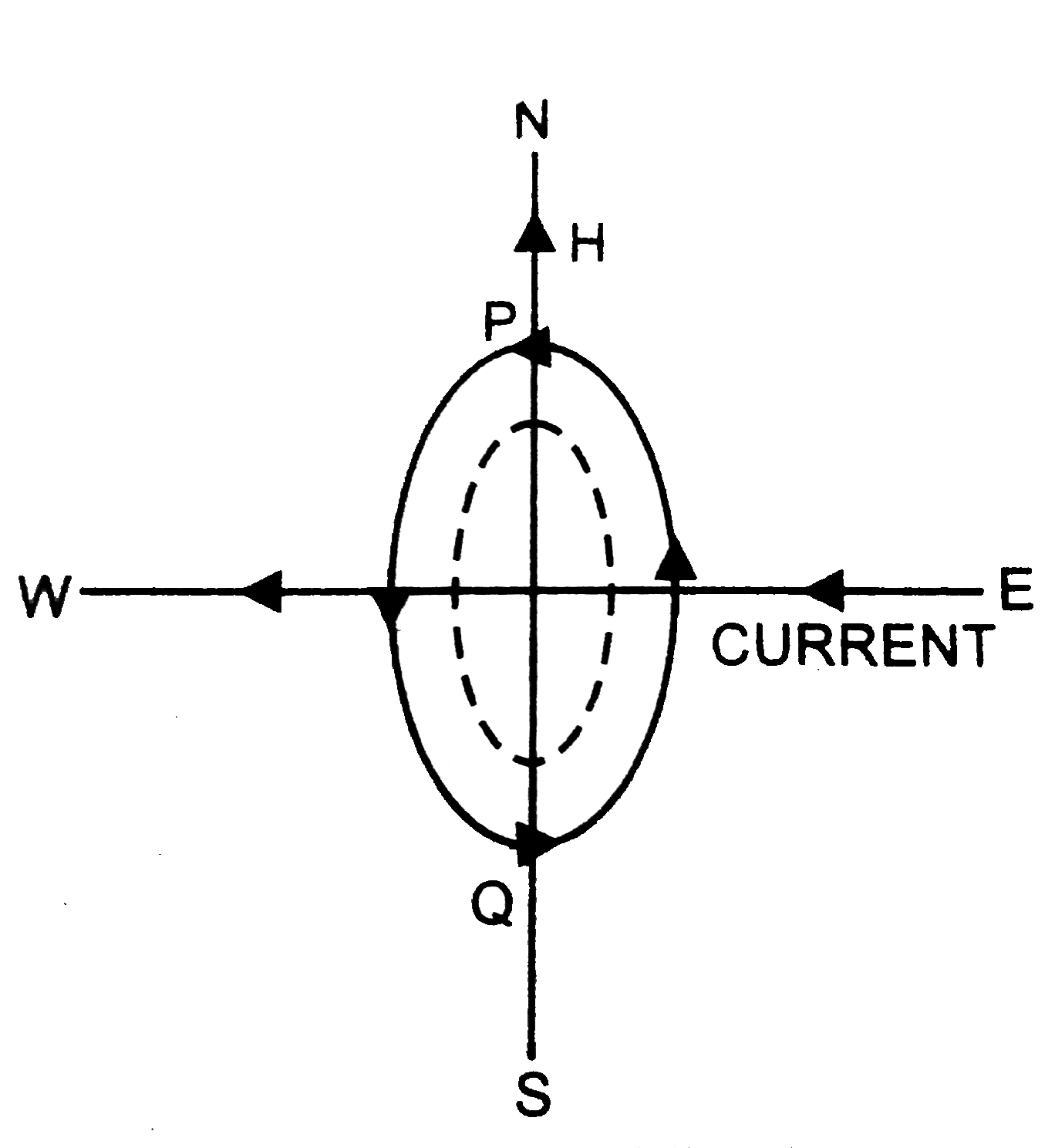A telephonic cable at a place has four long straight horizontal wires carrying a current of `1.0amp.` in the same direction east to west. The earth's magnetic field at the place is `0.39G` and the angle of dip is `35^@`. The magnetic declination is almost zero. What are the resultant magnetic fields at points `4.0cm` below and above the cable?

Explanation

Here, No. of wires, `n=4, i=1.0amp`., earth's field, `R=0.39G=0.39xx10^-4T`
dip, `delta=35^@`, declination `theat=0^@ R_1=? , R_2=?`,
`r=4cm` each `=4xx10^-2m`
Magnetic field at 4cm due to currents in 4 wires
`B=4xx(mu_0i)/(2pir)=4xx(4pixx10^-7xx1)/(2pixx4xx10^-2)=2xx10^-5tesla`
Horizontal component of earth's field
`H=Rcos delta=0.39xx10^-4cos35^@=0.39xx10^-4xx0.8192=3.19xx10^-5tesla`
Vertical component of earth's field
`V=R sin delta=0.39xx10^-4sin 35^@=0.39xx10^-4xx0.5736=2.2xx10^-5tesla`
At point Q, `4cm` below the wire, horizontal component due to earth's field and field due to current are in opposite directions, figure, so that `H_1=H-B`
`:. H_1=3.19xx10^-5-2xx10^-5=1.19xx10^-5tesla`
Hence, `R_1=sqrt(H_1^2+V^2)=sqrt((1.19xx10^-5)^2+(2.2xx10^-5)^2)`
`=2.5xx10^-5tesla`
At point P, 4cm above the wire, horizontal component of earth's field and field due to current are in the same direction, figure.
`:. H_2=H+B=3.19xx10^-5+2xx10^-5=5.19xx10^-5T`
`R_2=sqrt(H_2^2+V^2)=sqrt((5.19xx10^-5)^2+(2.2xx10^-5)^2)`
`=5.54xx10^-5tesla`