Five long wires A, B, C, D and E, each carrying current I are arranged to form edges of a pentagonal prism as shown in figure. Each carries current out of the plane of paper.
(a) What will be magnetic induction at a point on the axis O? Axis is at a distance R from each wire.
(b) What will be the field if current in one of the wires (say A) is switched off?
(c) What if current in one of the wire (say) A is reversed?

Explanation

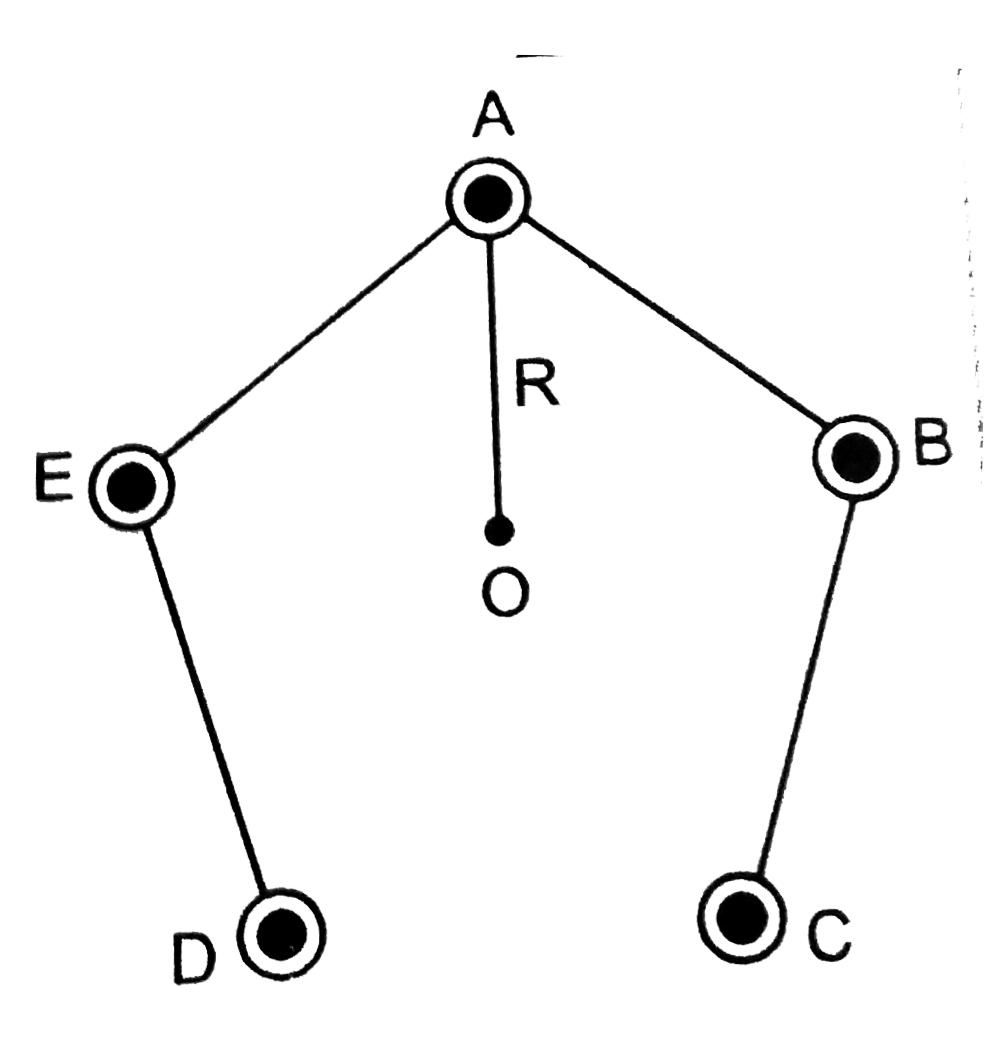
(a) Let the five wires A, B, C, D and E be perpendicular to the plane of paper at locations as shown in figure.
Resultant magnetic field induction at O due to current through all the five wires is `=0` (as magnetic field induction due to five wires will be represented by various sides of a closed pentagon in one order, lying in the plane of paper).
(b) Total Magnetic field induction at O due to currents through the wires A, B, C, D and E is equal and opposite to the magnetic field induction at O due to current through wire A.
`:.` Magnetic field induction at O due to current through wire A is
`B=(mu_0)/(4pi)(2I)/(R)` acting `_|_r` to `AO` towards right.
`:.` Magnetic field induction at O due to currents through the wires B, C, D and E is `=(mu_0)/(4pi)(2I)/(R)`, acting `_|_r` to `AO` towards left.
(c) If currrent in wire A is reversed, then total magnetic field induction at O
=mag. field induction due to wire A+mag. field induction due to wires B, C, D and E
`=(mu_0)/(4pi)(2I)/(R)` (acting `_|_r` AO towards left) +`(mu_0)/(4pi)(2I)/(R)` (acting `_|_r` AO towards left)
`=(mu_0I)/(piR)` acting `_|_r` AO towards left.