From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment `vecM`. Magnetic field induction at a point distance z from the magnetic dipole of moment `vecM(=Mhatk)` is
`|vecB|=(mu_0)/(4pi)(2|vecM|)/(z^3)=(mu_0M)/(2piz^3)`
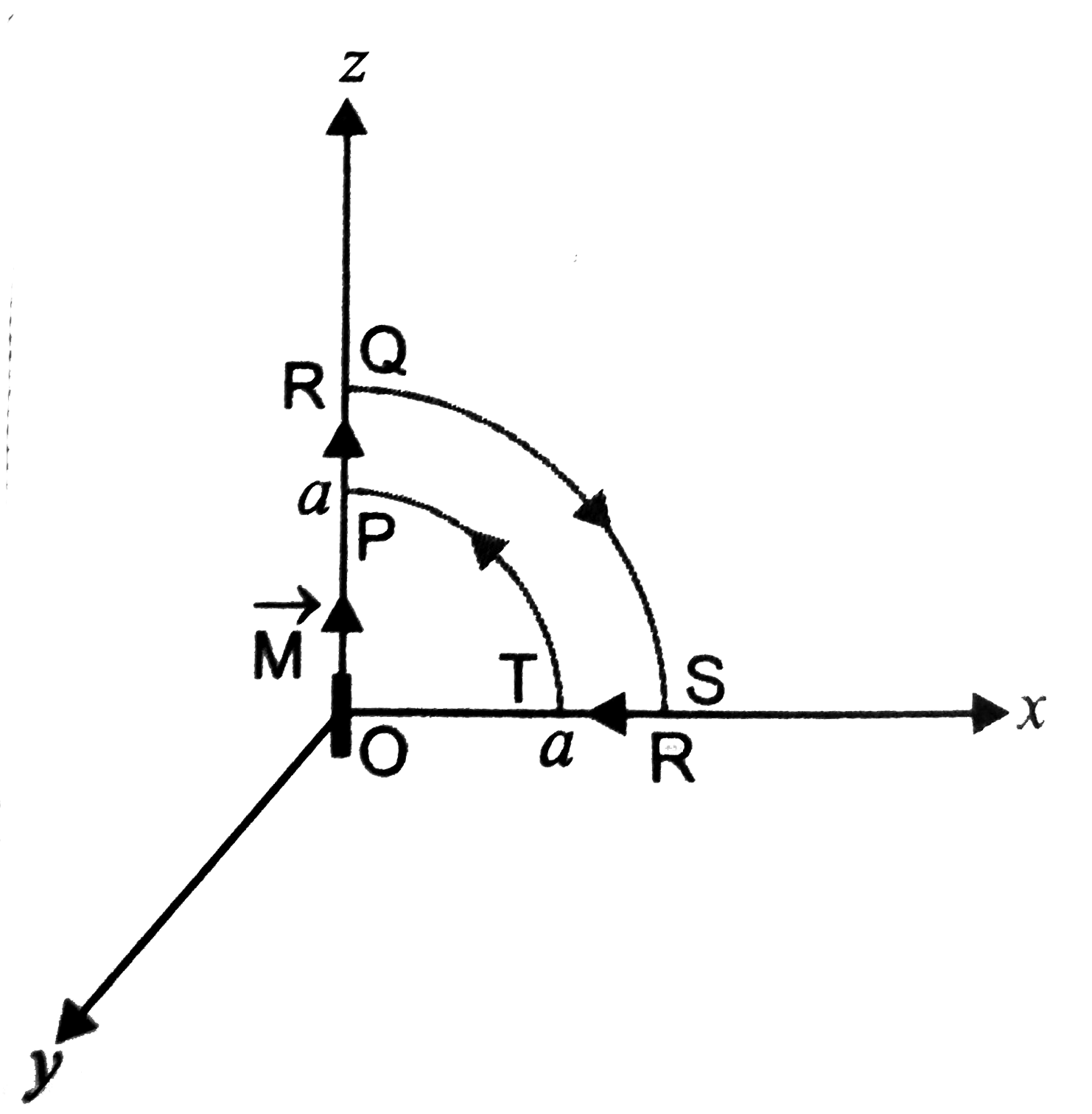
(i) Along z-axis from P to Q.
`int_(P)^(Q) vecB.dvecl=int_(P)^(Q) Bdlcos0^@=int_(a)^(R)Bdz`
`=int_(a)^(R)(mu_0)/(2pi)(M)/(z^3)dz=(mu_0M)/(2pi)(-1/2)(1/R^2-1/a^2)=(mu_0M)/(4pi)(1/a^2-1/R^2)`
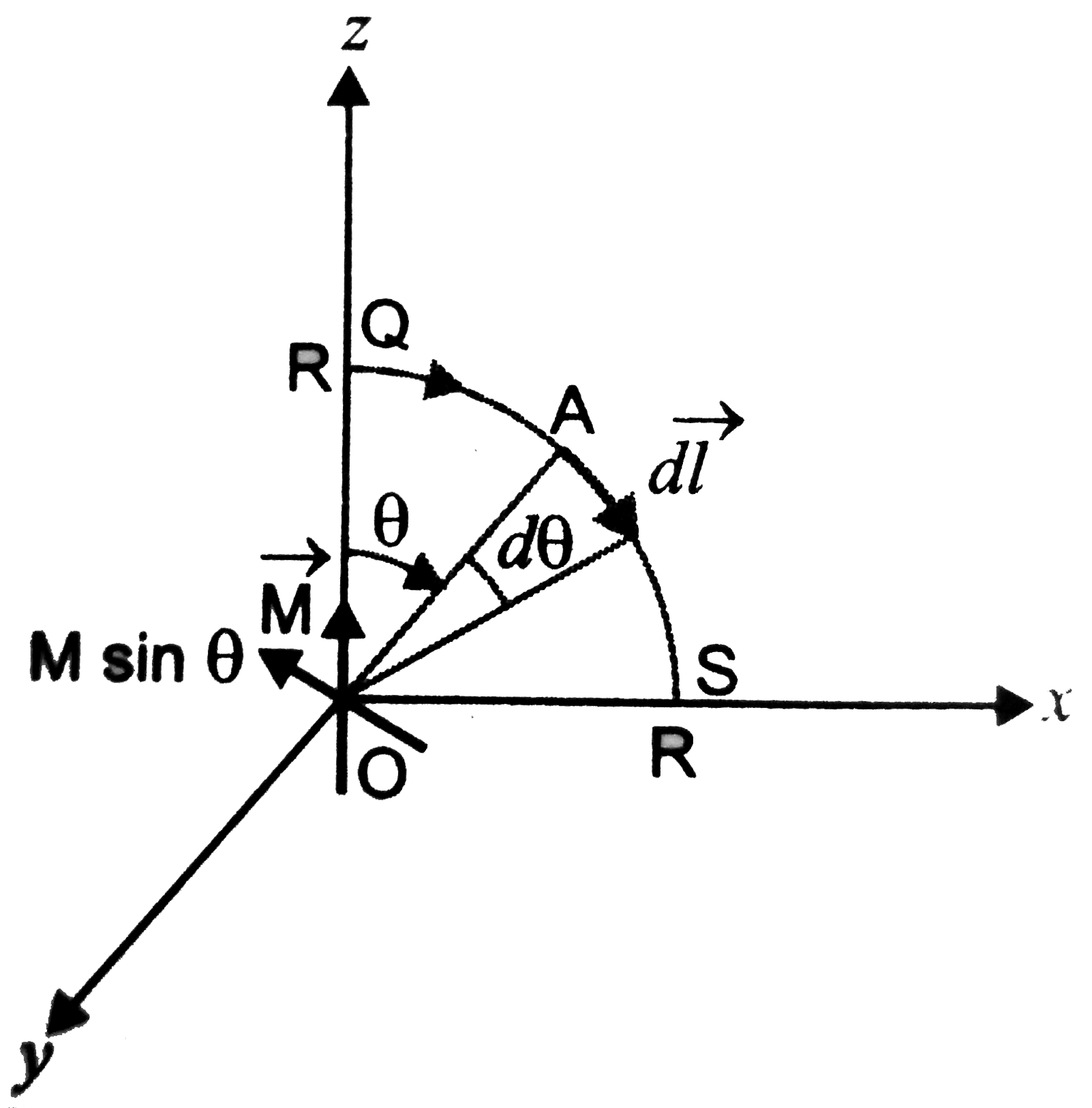
(ii) Along the quarter circle QS of radius R. point A lies on the equatorial line of the magnetic dipole of moment `M sin theta`
Magnetic field at point A on the circular arc is
`B=(mu_0)/(4pi)(Msintheta)/(R^3), dl=Rd theta`
`:. int_("circular arc" QS) vecB.dvecl=int Bdl cos 0=int_(0)^(pi//2) (mu_0)/(4pi)(Msintheta)/(R^3)Rd theta`
`=(mu_0)/(4pi)M/R^2(-cos theta)_0^(pi//2)=(mu_0)/(4pi)M/R^2`
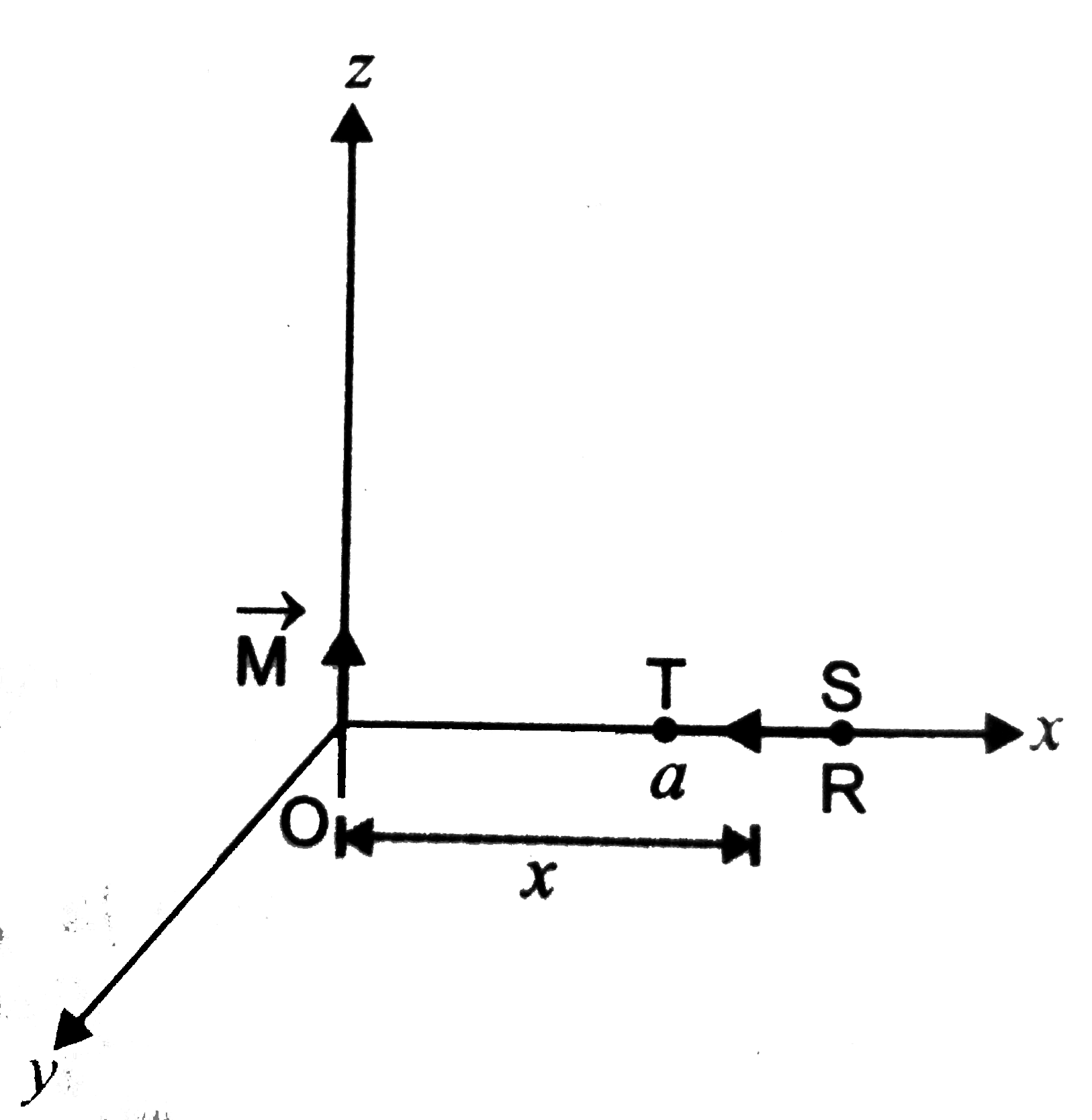
(iii) Along x-axis over the path ST. every point lies on the equatorial line of magnetic dipole. Magnetic field induction at a point distance x from the dipole is
`vecB=-(mu_0)/(4pi)(vecM)/(x^3)`
`:. int_(S)^(T) vecB.dvecl=int_(R)^(a)-(mu_0vecM)/(4pix^3).dvecl=0`
`[ :'` angle between `(-vecM)` and `dvecl` is `90^@`]
(iv) Along the quarter circle TP of radius a. (ii) Line integral of `vecB` along the quarter circle TP of radius a is
`int_("circular arc" TP) vecB.dvecl=int_(pi//2)^(0)(mu_0)/(4pi)(Msintheta)/(a^3)ad theta=(mu_0)/(4pi)(M/a^2)int_(pi//2)^(0)sint heta d theta`
`=(mu_0)/(4pi)M/a^2[-cos theta]_(pi//2)^0=-(mu_0)/(4pi)M/a^2`
`:. oint_(PQST)vecB.dvecl=int_(P)^(Q)ecB.dvecl+ int_(Q)^(S)vecB.dvecl+int_(S)^(T)tvecB.dvecl+ int_(T)^(P)vecB.dvecl`
`=(mu_0M)/(4pi)[1/a^2-1/R^2]+(mu_0)/(4pi)(M)/(R^2)+0+(-(mu_0)/(4pi)M/a^2)=0`




