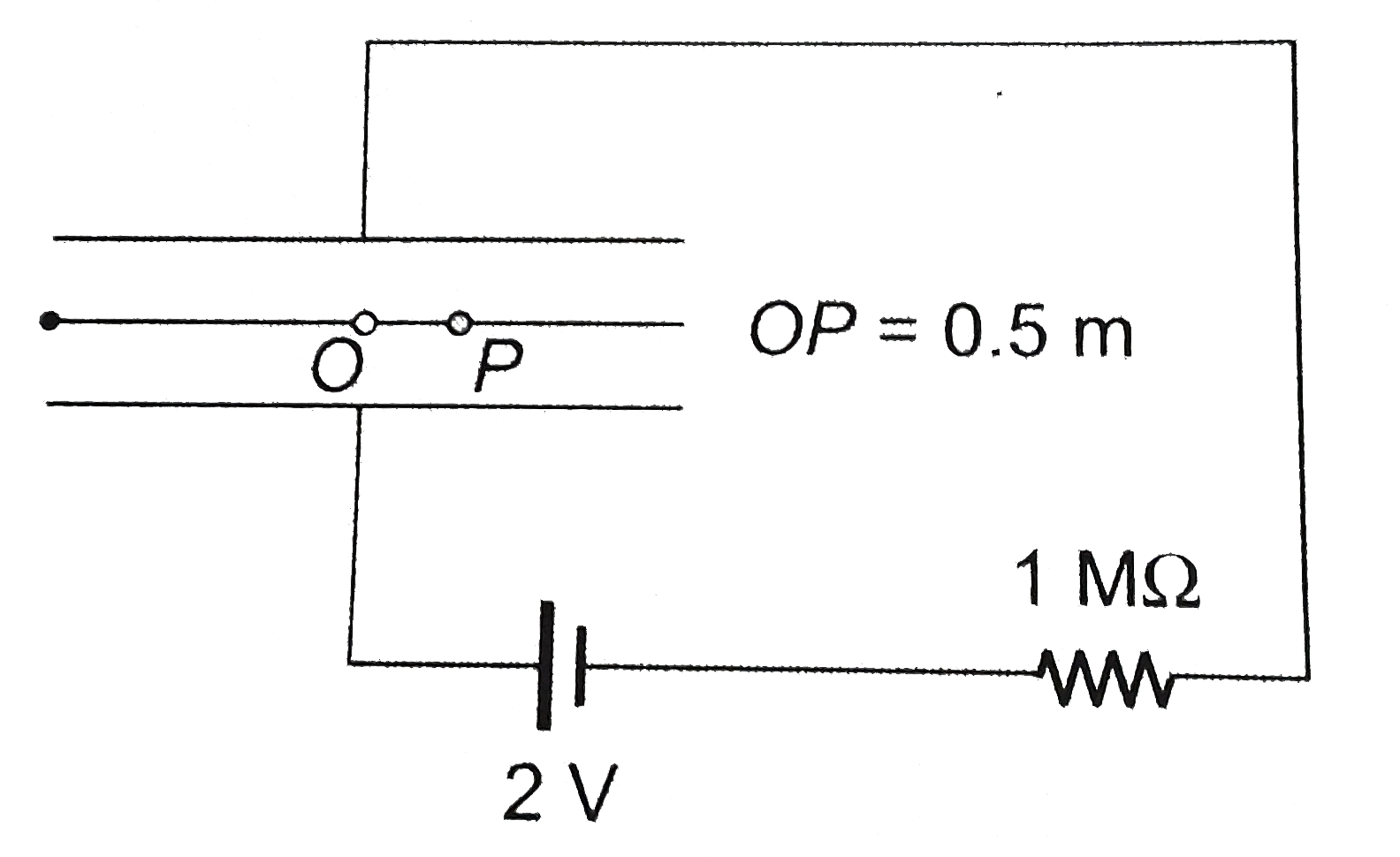
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PRADEEP-ELECTROMAGNETIC WAVES-II Focus multiple choice question
- A parallel plate capacitor with circular plates of radius 1m has a cap...
Text Solution
|
- Which of the following Maxwell's equations have sources of vecE and ve...
Text Solution
|
- When a capacitor of capacitance C after charging with a charge Q is co...
Text Solution
|
- When a capacitor of capacitance C after charging with a charge Q is co...
Text Solution
|
- When a capacitor of capacitance C after charging with a charge Q is co...
Text Solution
|
- The sun delivers 10^3W//m^2 of electromagnetic flux to the earth's sur...
Text Solution
|