(a) Explain with reason, how the power of a diverging lens changes when (i) it is kept in a medium of refractive index greater than that of the lens, (ii) incident red light is replaced by violet light.
(b) Three lenses `L_(1), L_(2), L_(3)` each of focal length 30 cm are placed co-axially as shown in the figure. An object is held at 60 cm from the optic centre of lens `L_(1)`. The final real image is formal at the focus of `L_(3)`. Calculate the separation between (i) `(L_(1) and L_(2)) and " (ii) " (L_(2) and L_(3))`.

Explanation

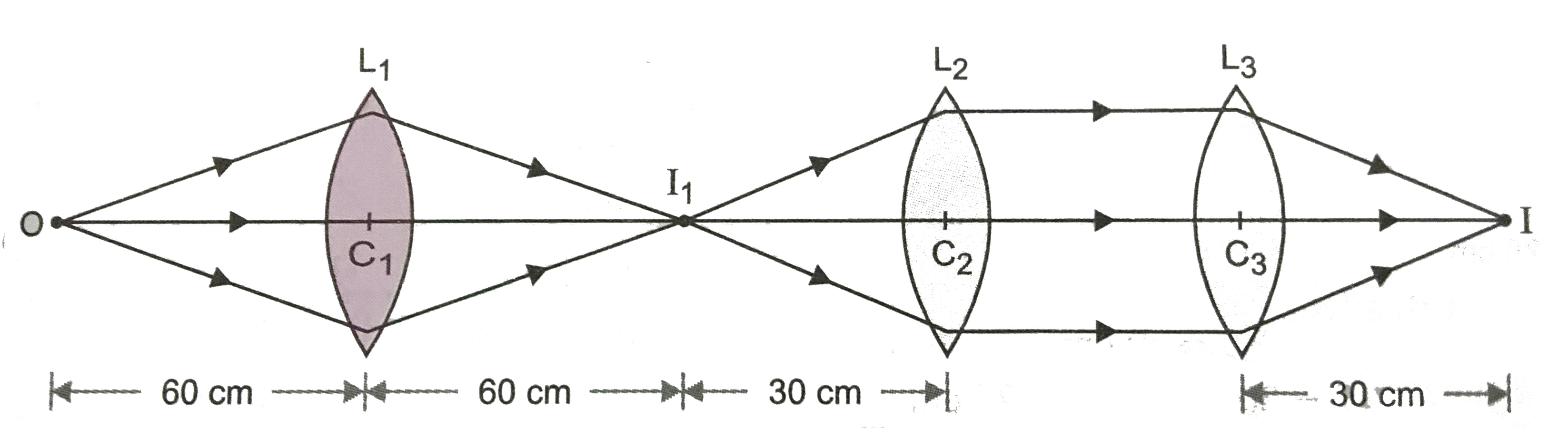
For lens `L_(1)` , `u = - 60cm, f = + 30cm`.
If `v_(1)` is distance of image `I_(1)` from `C_(1)`, then from
`(1)/(v_(1)) - (1)/(u) = (1)/(f_(1))`
`(1)/(v_(1)) = (1)/(f_(1)) + (1)/(u) = (1)/(30) - (1)/(60) = (1)/(60)`
`v_(1) = 60 cm = C_(1)I_(1)`.
As final image `I` is at focus of `L_(3)`, therefore, rays falling on `L_(3)` must be parallel to commen principal axis. For this to happen, `I_(1)` must be at the focus of `L_(2)`. Hence distance between `L_(1)L_(2)` is
`= C_(1)C_(2) = C_(1)I_(1) + I_(1)C_(2) = 60 cm + 30 cm = 90 cm`
and distance between `L_(2)` and `L_(3)` can have any reasonable value, as rays between `L_(2)` and `L_(3)` are parallel rays. The course of rays is shown in Fig.