Find the position of the image formed by the lens combination given in Fig.
.

Explanation

For 1st lens,
`u_(1) = - 30 cm, f_(1) = + 10 cm, v_(1) = ?`
As `(1)/(v_(1)) - (1)/(u_(1)) = (1)/(f_(1)) :. (1)/(v_(1)) - (1)/(-30) = (1)/(10)`

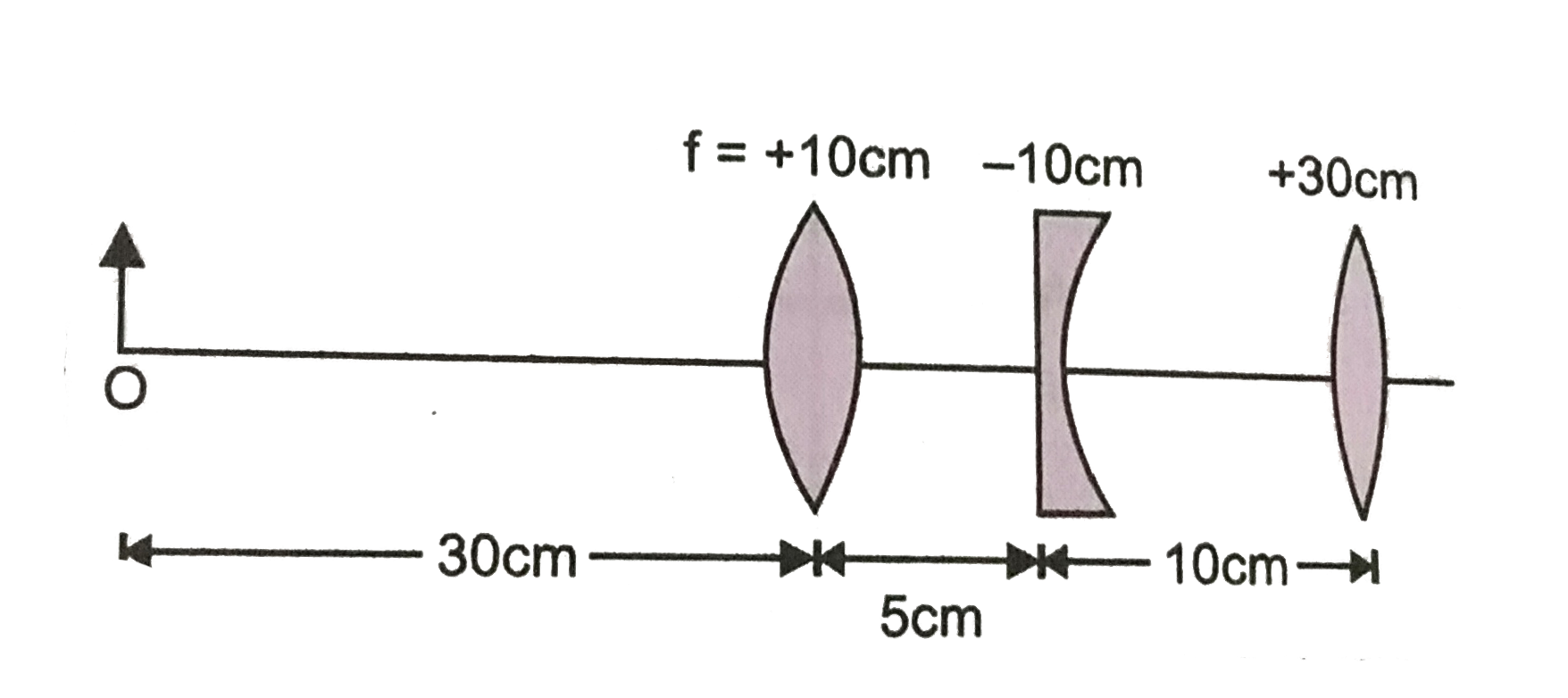
`(1)/(v_(1)) = (1)/(10) - (1)/(30) = (1)/(15), v_(1) = 15 cm`.
Image formed by first lens serves as object for second lens at a distance `= (15 - 5) = 10 cm` to the right of second lens, and the object is virtual.
Therefore, for second lens,
`u_(2) = 10 cm, v_(2) = ? f_(2) = - 10 cm`.
As `(1)/(f_(2)) = (1)/(v_(2)) - (1)/(u_(2)) :. -(1)/(10) = (1)/(v_(2)) - (1)/(10)`
`:. (1)/(v_(2)) = 0, v_(2) = oo`.
The virtual image is formed at infinity to the right of 2nd lens. This acts as an object for 3rd lens.
Therefore, for 3rd lens, `u_(3) = oo, v_(3) = ?`
`f_(3) = + 30 cm`.
As `(1)/(v_(3)) - (1)/(u_(3)) = (1)/(f_(3))`
`:. (1)/(v_(3)) - (1)/(oo) = (1)/(30)` or `v_(3) = 30 cm`.
The final image is formed at `30 cm` to the right of third lens.