A ray of light enters the face `AB` of a glass prism of refractive index `mu` at an angle of incidence `i`. Find the value of `i` such that no ray emerges from the face `AC` of the prism, given angle of prism is `A`.

Explanation

As shown in Fig. no ray will emerge from face `AC` of the prism, when light undergoes total internal reflection at `R` for which, `r_(2) = C`, the critical angle.
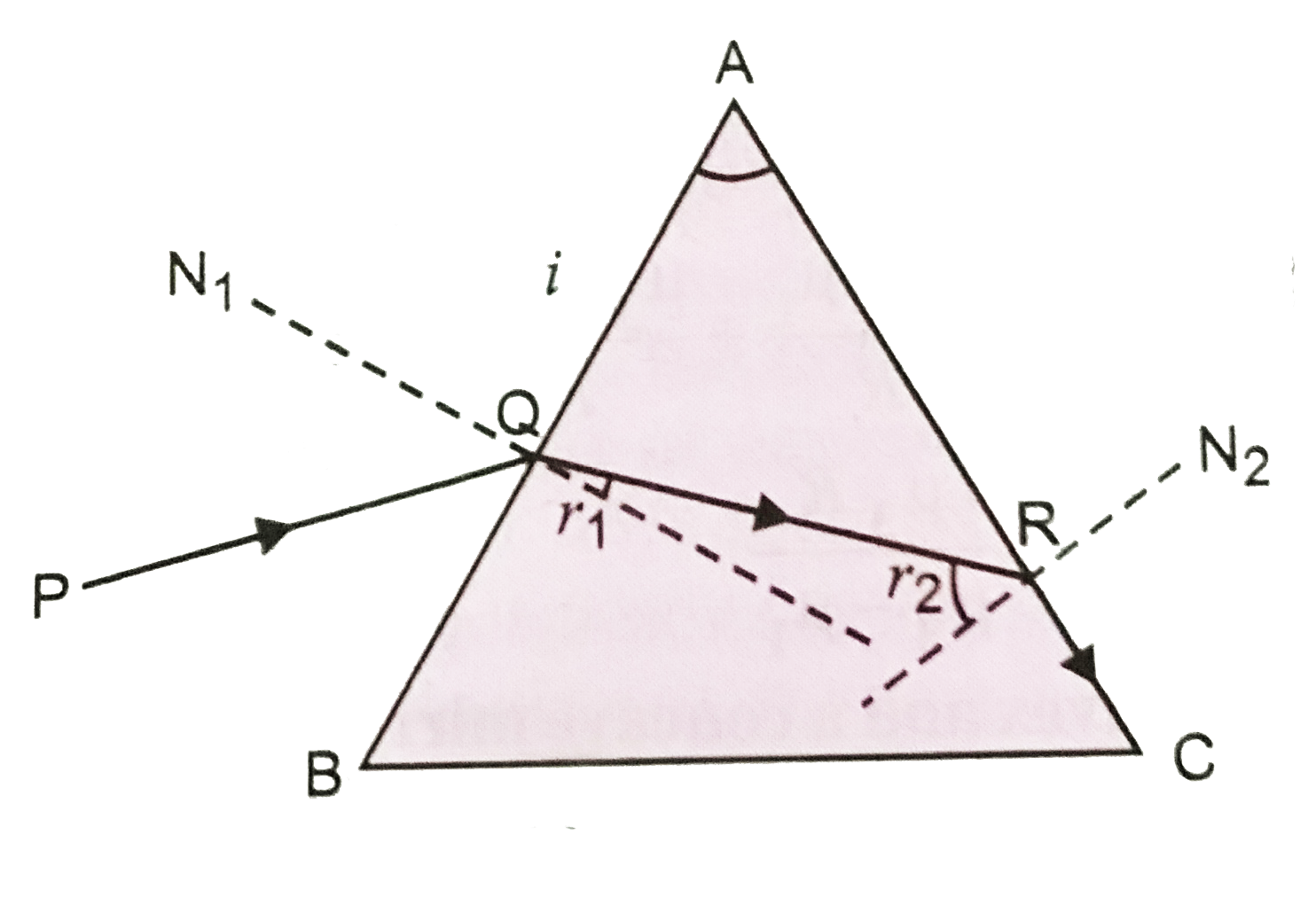
ltbr. As `sin C = (1)/(mu) = sin_(2)`
`:. mu sin r_(2) = 1` ...(i)
As `r_(1) + r_(2) = A, r_(1) = A - r_(2)`
From Snell's Law,
`sin i = mu sin r_(1) = mu sin (A - r_(2))`
`= mu(sin A cos r_(2) - cos A sin r_(2))`
`sin i = mu sin A cos r_(2) - mu sin r_(2) cos A`
using (i), `sin i = mu sin A cos r_(2) - cos A` ... (iii)
From (i), `sin r_(2) = (1)/(mu)`
`:. cos r_(2) = sqrt(1 - sin^(2) r_(2)) = sqrt(1 - (1)/(mu^(2))`
Put in (iii),
`sin i = mu sin A sqrt(1 - (1)/(mu^(2)) - cos A`
Hence, `i = sin^(-1)[mu sin A sqrt(1- 1/(mu^(2))) - cos A]`