A gaint refrecting telescope at an observatory has an objective lens of focal length `15 m`. If an eye piece lens of focal length `1 cm` is used, find the angular magnification of the telescope.
If this telescope is used to view the moon, what is the diameter of image of moon formed by objective lens ? The diameter of the moon is `3.42 xx 10^6 m` and radius of lunar orbit is `3.8 xx 10^8 m`.

Explanation

Here, `f_(0) = 15 cm, f_(e) = 1.0 cm = 10^(-2)m`
(a) Angular magnification `= (-f_(0))/(f_(e)) = (-15)/(10-^(-2)) = - 1500`
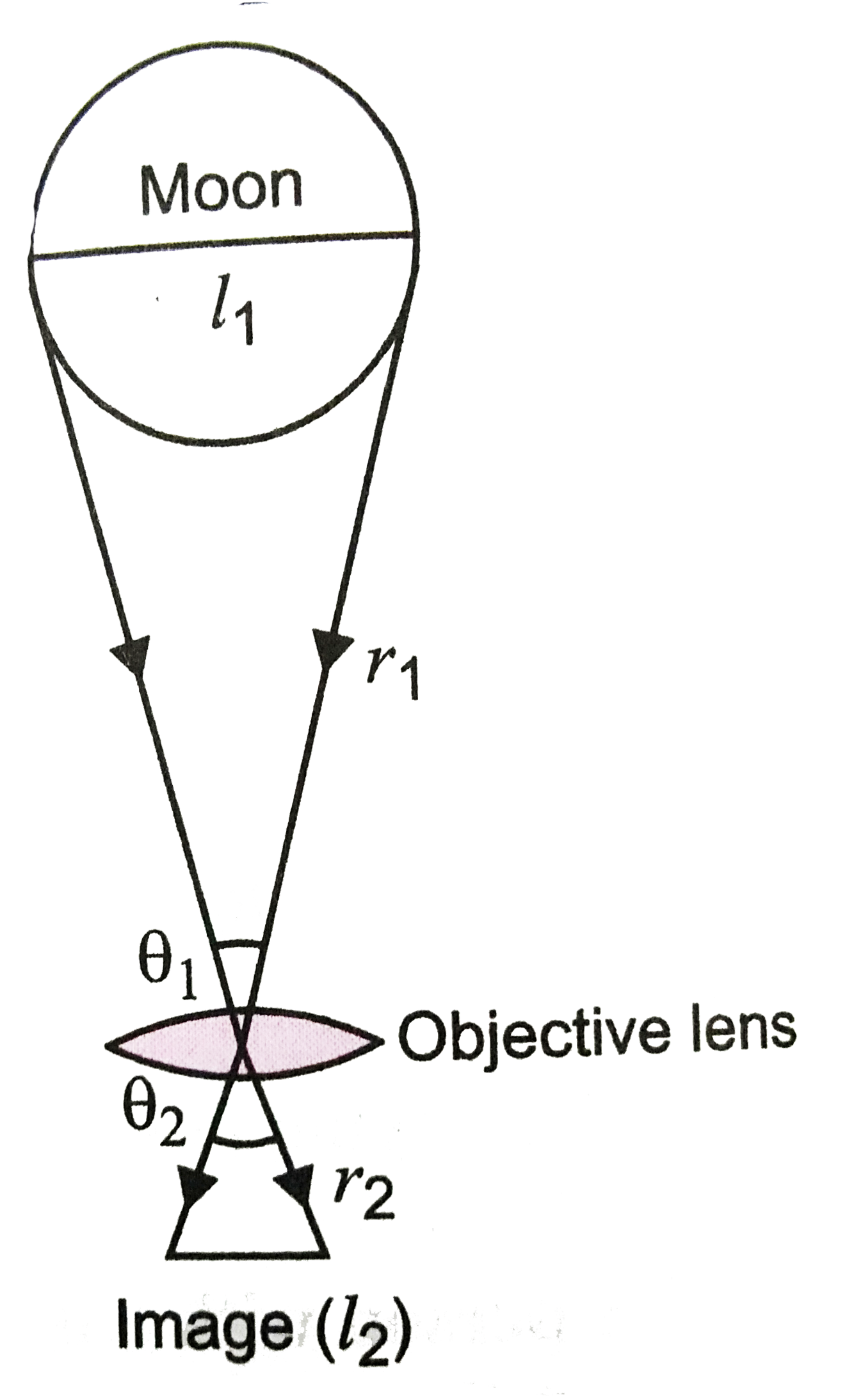
(b) If `d` diameter of the image, then from Fig.
angle subtended by diameter of moon `theta_(1) = (l_(1))/(r_(1)) = (3.48 xx 10^(6))/(3.8 xx 10^(8))`
and, angle subtended by image `theta_(2) = (l_(2))/(r_(2)) = (d)/(f_(0)) = (d)/(15)`
As `thta_(2) = theta_(1) :. (d)/(15) = (3.48 xx 10^(6))/(3.8 xx 10^(8))`
`d = (3.48 xx 15 xx 10^(-2))/(3.8)`
`= 13.73 xx 10^(-2)m = 13.73 cm`