Home
Class 12
PHYSICS
In may experimental set-ups the source a...

In may experimental set-ups the source and screen are fixed at a distance say `D` and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.

Text Solution

Verified by Experts

In the lens formula, `(1)/(f) = (1)/(v) - (1)/(u)`
We find that u and v reversible. Therefore, there are two positions of the object, for which there will an image on the screen.
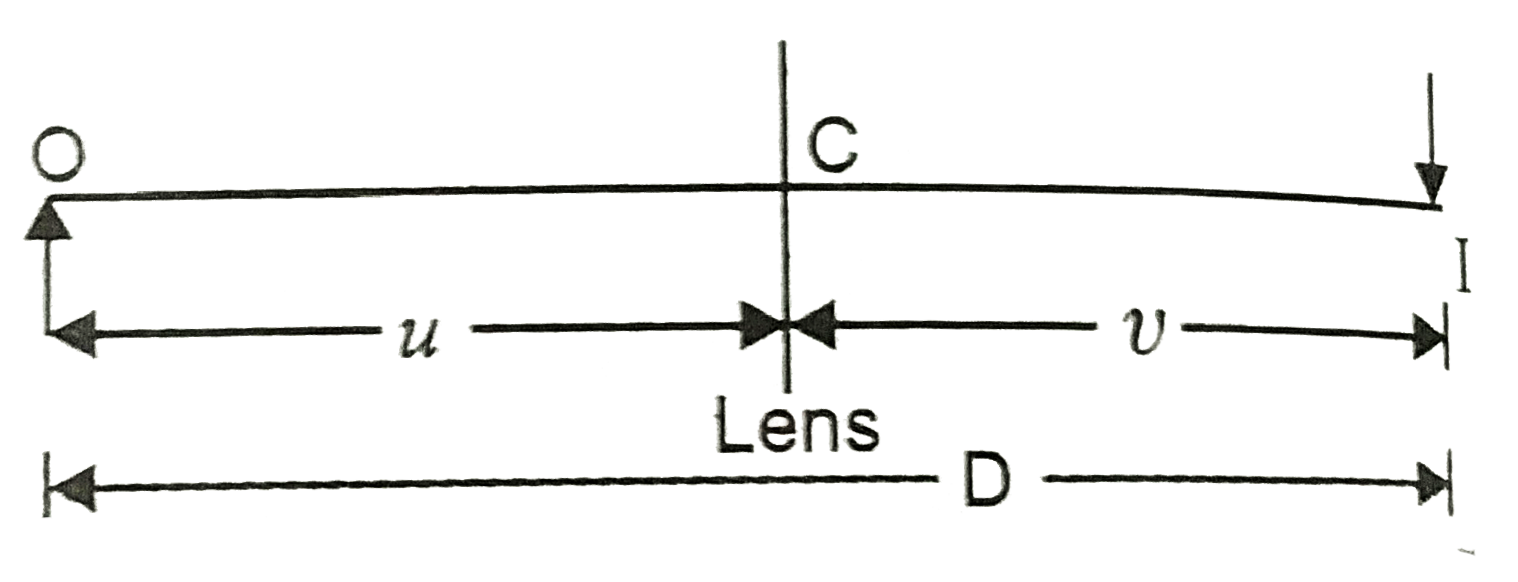
Let the first position be when lens is at `C`, Fig.
`:. -u + v = D =` distance between source (O) and screen I.
or `u = - (D - v)`
Put in (i)
`(1)/(v) + (1)/(D - v) = (1)/(f) or (D - v +v)/(v(D - v)) = (1)/(f) or D v - v^(2) = Df or v^(2) - Dv + Df = 0`.
`:. v = (D +- sqrt(D^(2) - 4 Df))/(2) = (D)/(2)+- (sqrt(D^(2) - 4 Df))/(2) and u = - (D - v) = [(D)/(2)+-(sqrt(D^(2) - 4 Df))/(2)]`
Thus if object distance is `u = (D)/(2) + (sqrt(D^(2) - 4 Df))/(2)`, then image distance is `v = (D)/(2) - (D)/(2) - (sqrt(D^(2) - 4 Df))/(2)`
Again, if object distance is `u = (D)/(2) - (sqrt(D^(2) - 4 Df))/(2)` , then image distance is `v = (D)/(2) + (sqrt(D^(2) - 4 Df))/(2)`
The distance between two position of the lens for these two object distance is
`d = (D)/(2) +(sqrt(D^(2) - 4 Df))/(2) - (D)/(2) + (sqrt(D^(2) - 4 Df))/(2) = sqrt)(D^(2) - 4 Df)`
If `u = (D)/(2) + (d)/(2)`, then `v = (D)/(2) - (d)/(2) :.` magnification, `m_(1) = (v)/(u) = (D - d)/(D + d)`
If `u = (D)/(2) - (d)/(2)`, then `v = (D)/(2) + (d)/(2) :.` magnification, `m_(2) = (v)/(u) = (D + d)/(D - d)`.
Promotional Banner

Topper's Solved these Questions

  • OPTICS

    PRADEEP|Exercise Very short answer question|5 Videos

  • OPTICS

    PRADEEP|Exercise very short answer questions|1 Videos

  • MAGNETIC EFFECT OF CURRENT AND MAGNETISM

    PRADEEP|Exercise Competition Focus (Multiple Choice Questions)|2 Videos

Similar Questions

Explore conceptually related problems

An object and a screen are kept at a distance of 120 cm A lens of focal length 22.5 cm is kept between them so that a real image is formed on the screen Find the possible location (s) of the lens.

A thin converging lens is placed between an object and a screen whose position are fixed. There are two positions of the lens at which the sharp image of the object is formed on the screen. Find the transverse dimension of the object if at one position of the lens the image dimension equal h' = 2.0 mm and at the other, h'' = 4.5 mm .

A thin convergent lens is placed between an object and a screen whose positions are fixed. There are two positions of a lens at which sharp image of the object is formed on the screen. If the size of the images in the two cases are 2 mm and 4.5 mm then the size of the object should be:-

A convex lens forms a real image on a screen placed at a distance 60 cm from the object. When the lens is shifted towards the screen by 20 cm , another image of the object is formed on the screen. The focal length of the lens is :

An object and a screen are placed 80 cm apart. There are two positions at which a convex lens forms a real image on the screen, the magnification in the cases being 3/2 and 2/3. Calculate the focal length of the lens.

The distance between the object and the screen is d (greater than 4 times the focal length of a convex lens). Real images of the object are obtained on the screen for two positions of the lens that are separated by distance x apart. The ratio of size of the images in the two positions of the lens are

A convex lens is placed between an object and a screen which are at a fixed distance apart for one position of the lens. The magnification of the image obtained on the screen is m_(1) . When the lens is moved by a distance d the magnification of the image obtained on the same screen m_(2) , Find the focal length of the lens.