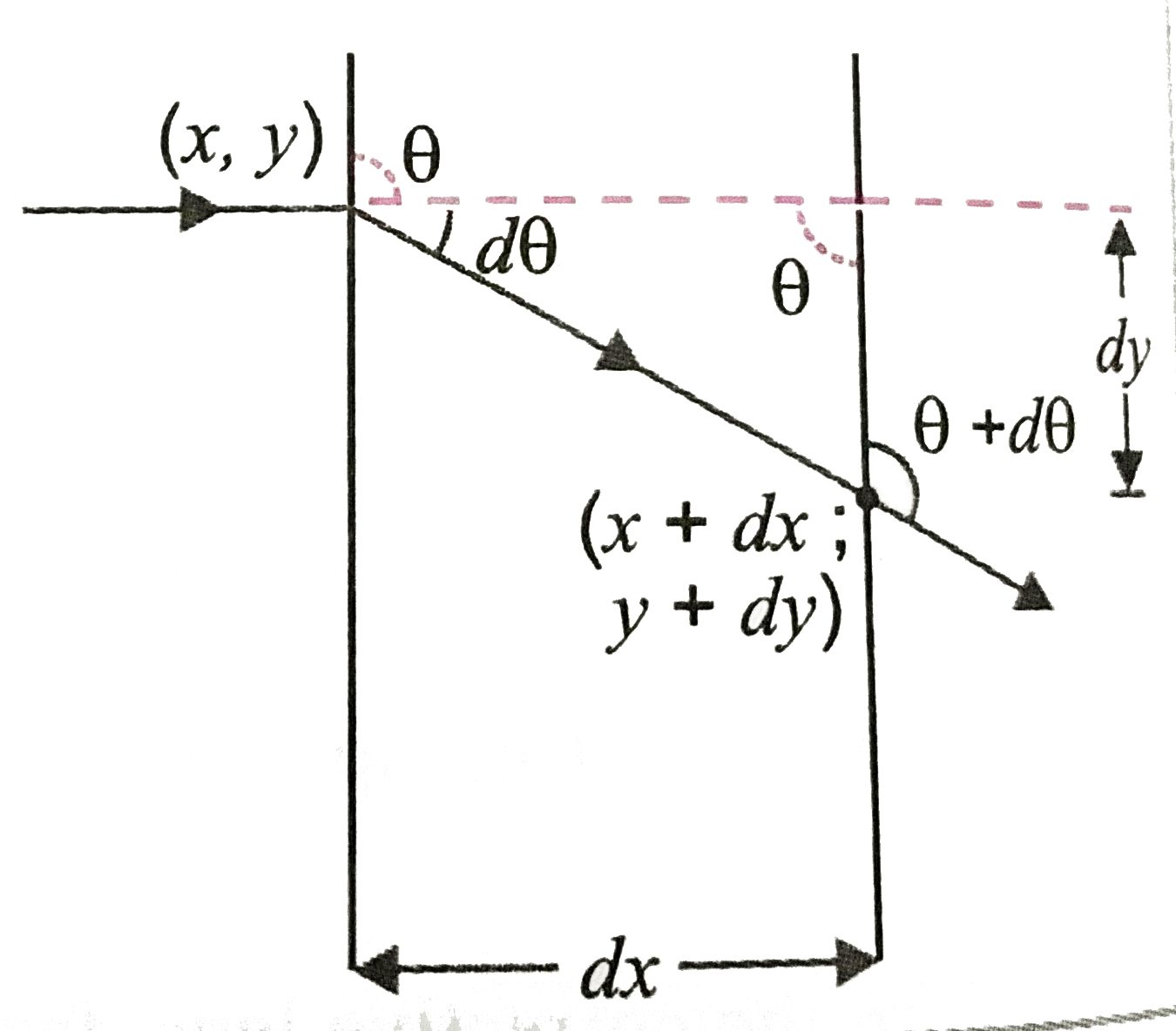The mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions `lt lt` vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance `d lt lt h`, the height of the column.

Explanation

In Fig. we have shown a ray of light entering the column at (x, y) at `90^(@)` to the vertical. A portion of ray between x and `(x + dx)` deviates through an angle `d theta`, emerging at `(x + dx, y + dy)` at angle `(theta + d theta)`, while the angle at the entry is `theta`.
According to Snell's law,
`mu(y) sin theta = mu(y + dy)sin (theta + dtheta)`
`= [(mu(y) + (dmu)/(dy)dy)] (sin theta cos d theta + cos theta sin d theta)`
As `d theta` is small, `cos d theta ~~ 1` and `sin d theta = d theta`.
`:. mu(y) sin theta ~~ mu(y) sin theta + mu(y) cos theta d theta + (d mu)/(dy)dy sin theta` (fourth term is negligible small)
`mu(y) cos theta d theta = -(d mu)/(dy)dy sin theta`
`d theta = -(1)/(mu)(d mu)/(dy) dy tan theta`
From Fig. `tan theta = (dx)/(dy) or dy tan theta = dx`
`d theta = -(1)/(mu)(d mu)/(dy) dx`
`theta = -(1)/(mu)(dmu)/(dy)int_(0)^(d) dx = -(1)/(mu)(dmu)/(dy)(d)`
This is the required deviation in travelling a horizontal distance `d`.