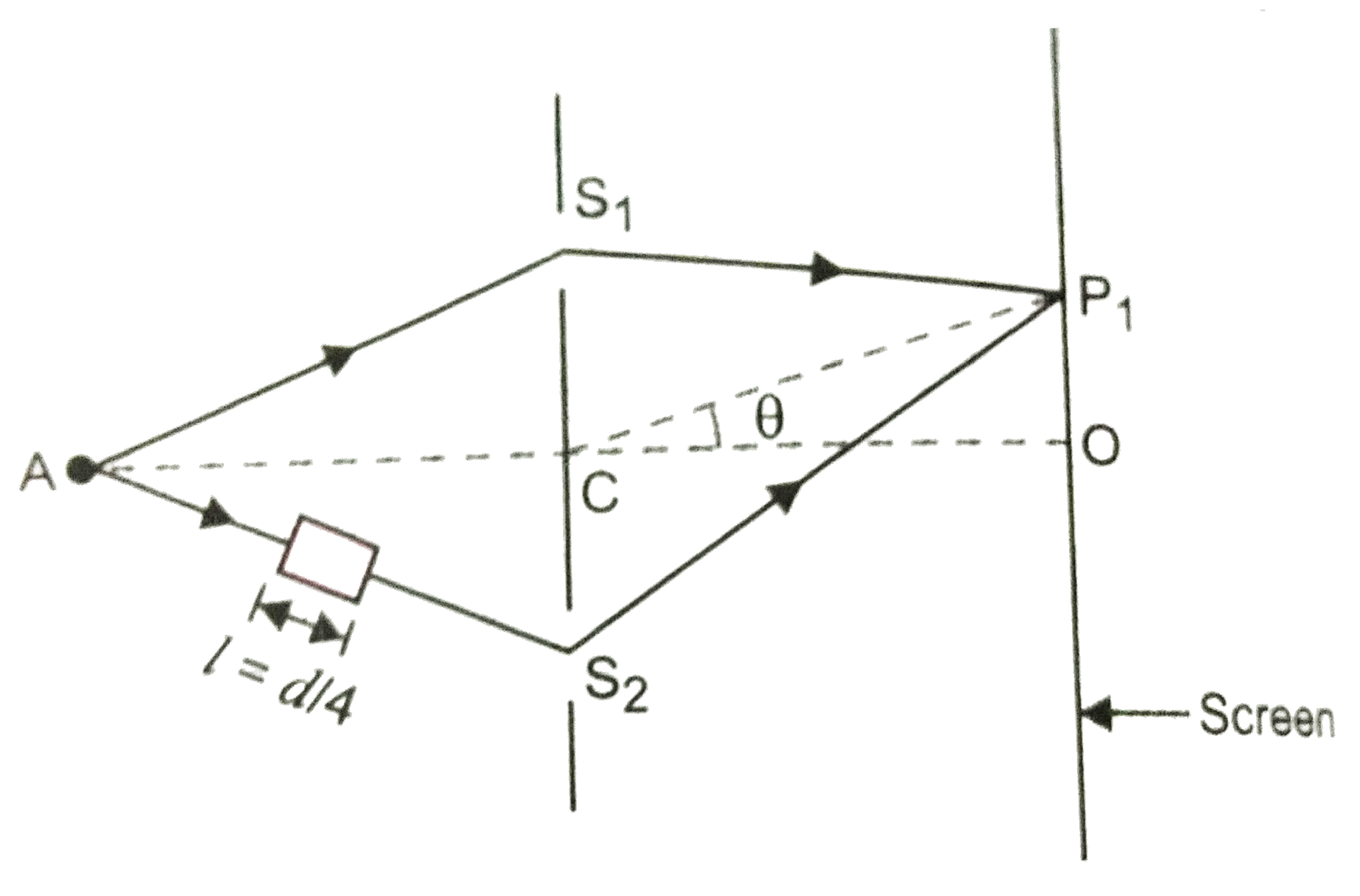
A small transparent slab `(mu = 1.5)` is placed along `AS_(2)` as shown.

`AC=CO=D,S_(1)C=S_(2)S=d lt ltD`
The distance of princpal maxima front 'O' is

Explanation

As is clear from Fig. path difference between waves reaching `P_(1)` from A is
`= 2d sin theta + (mu - 1)l`.
For principal maximum, path diff. `= 0`.
i.e., `2d sin theta + (mu - 1) l = 0`
`2d = sin theta + (1.5 - 1)(d)/(4) = 0 , sin theta = (-1)/(16)`
`:. OP_(1) = (CO) tan theta ~= D(-(1)/(16))`
For the first minimum, a angle `theta_(1)`, say,
path difference `= 2 d sin theta_(1) + 0.5 l = +- lambda//2`
`sin theta_(1) = (+- lambda//2 - 0.5 l)/(2d)`
As diffraction ocuurs when `d = lambda, :. sin theta_(1) = (+- lambda//2 - lambda//8)/(2 lambda) = +-(1)/(4) - (1)/(16)`
on the positive side, `sin theta_(1) = + (1)/(4) - (1)/(16) = (3)/(16)` , on the negative side, `sin theta'_(1) = -(1)/(4) - (1)/(16) = (-5)/(16)`.
The first principal maximum on the positive side is at distance (above `O`)
`= D than theta_(1) = D (sin theta_(1))/(sqrt(1 - sin^(2) theta_(1))) = (D.3//16)/(sqrt 1 - 9//256) = (3D)/(sqrt(16^(2) - 3^(2))`
On the negative side, distance of first principal maximum (below `O`) will be
`= D theta'_(1) = D (sin theta'_(1))/(sqrt(1 - sin^(2) theta_(1))) = (D(-5//16))/(sqrt (1 - (5//16))^(2)) = (-5D)/(sqrt(16^(2) - 5^(2))`