Four identical monochromatic source A, B, C, D as shown in figure produce waves of the same wavelength `lambda` and are coherent. Two receivers `R_(1)` and `R_(2)` are at great but equal distance from B. The choose the correct statements.

Four identical monochromatic source A, B, C, D as shown in figure produce waves of the same wavelength `lambda` and are coherent. Two receivers `R_(1)` and `R_(2)` are at great but equal distance from B. The choose the correct statements.


Text Solution
Verified by Experts
In Fig. A, B, C, D are four idential monochromatic coherent sources producing waves of same wavelength `lambda`.
`AB = BC = BD = lambda//2`.
`R_(1)` and `R_(2)` are two receivers held as shown such that `R_(1)B = R_(2)B = d (gt gt lambda)`.
Let the wave at `R_(1)` from `B and A = lambda//2` so that phase diff. is `pi`.
`:.` The wave at `R_(1)` because of source `B` is
`y_(B) = a cos (omega t - pi) = - a cos omega t`
Similarly, path diff. of singal at `R_(1)` from C and A `= lambda` so that phase diff. `= 2pi`
`:.` The wave at `R_(1)` because of source `C` is
`y_(C) = a cos (omega t - 2pi) = a cos omega t`
Again, path diff. of signal at `R_(1)` From `D` that of `A` is
`= sqrt(d^(2) + ((lambda)/(2))^(2)) - d(d - lambda//2) = d (1 + (lambda^(2))/(4 d^(2)))^(1//2) - d + (lambda)/(2) = d(1 + (lambda^(2))/(8 d^(2))) - d + (lambda)/(2) ~= (lambda)/(2)` (`because d gt gt lambda`)
Therefore, phase diff. is `pi`
`y_(D) = a cos (omega t - pi) = - a cos omega t`
Hence the signal picked up at `R_(1)` from all the four sources is
`y_(R_(1)) = y_(A) + y_(B) + y_(C) + y_(D) = a cos omega t - a cos omega t + a cos omega t - a cos omega t = 0`. ...(i)
Let the the signal picked up at `R_(2)` from to be `y_(B) = a_(1) cos omega t`
Path differecne of signals at `R_(2)` from `D` to that from `B` is `lambda//2`. Therefore, `y_(D) = a_(1) cos (omega t - pi)`
`= - a_(1) cos omega t`.
Again, path diff. of signals at `R_(2)` from `B` and `A` is
`= sqrt(d^(2) + (lambda//2)^(2)) - d = d (1 + (lambda^(2))/(4 d^(2)))^(1//2) -d = (1)/(8)(lambda^(2))/(d^(2))`
As `d gt gt lambda`, therefore this path diff. `rarr 0`, and phase diff. `phi rarr 0 :. y_(A) = a_(1) cos (omega t - phi)`
Similarly, `y_(C) = a_(1) cos (omega t - phi)`
Hence the signal picked up at `R_(2)` from all the four sources is
`y_(R_(2)) = y_(A) + y_(B) + y_(C) + y_(D) = a_(1) cos (omega t - phi) + a_(1) cos omega t + a_(1) cos (omega t - phi) - a_(1) cos omega t`
`y_(R_(2)) = 2 a_(1) cos (omega t - phi)` ...(ii)
Hence receiver `R_(2)` picks up the larger signal.
(ii) If source `B` is swithched off, then from (i),
`y_(R_(1)) = a cos omega t lt I_(R_(1)) gt = a^(2) lt cos^(2) omega t gt = (a^(2))/(2)`
From (ii), `y_(R_(2)) = a_(1) cos (omega t - phi) = a_(1) cos omega t, because phi rarr 0 lt I_(R_(2)) gt = a_(1)^(2) lt cos^(2) omega t gt = (a_(1)^(2))/(2) = (a^(2))/(2)`.
Hence `R_(1)` and `R_(2)` pick up the same signal.
(iii) When source `D` is swithched off, `Y_(R_(1)) = a cos omega t`
`:. lt I_(R_(1)) gt = (a^(2))/(2)` and `y_(R_(2)) = 3a cos omega t` (Taking `phi rarr 0`)
`lt I_(R_(2)) gt = 9 a^(2) lt cos^(2) omega t gt = (9)/(2)a^(2)` `:. R_(2)` picks up larger signal compared to `R_(1)`.
(iv) Hence a signal at `R_(1)` indicates that source `B` has been switched off and an anhanced signal at `R_(2)` indicates that source `D` has been switched off.
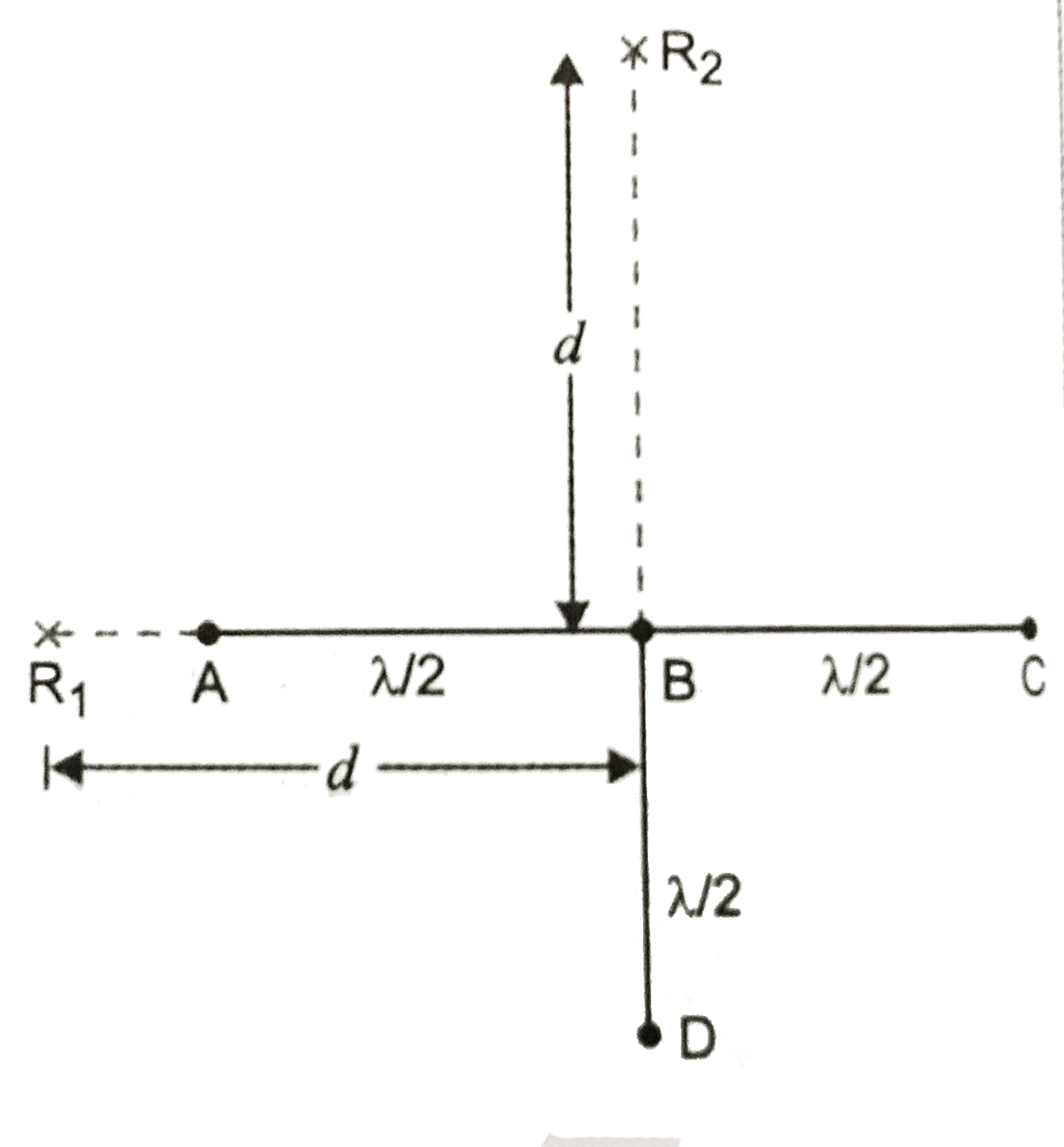
`AB = BC = BD = lambda//2`.
`R_(1)` and `R_(2)` are two receivers held as shown such that `R_(1)B = R_(2)B = d (gt gt lambda)`.
Let the wave at `R_(1)` from `B and A = lambda//2` so that phase diff. is `pi`.
`:.` The wave at `R_(1)` because of source `B` is
`y_(B) = a cos (omega t - pi) = - a cos omega t`
Similarly, path diff. of singal at `R_(1)` from C and A `= lambda` so that phase diff. `= 2pi`
`:.` The wave at `R_(1)` because of source `C` is
`y_(C) = a cos (omega t - 2pi) = a cos omega t`
Again, path diff. of signal at `R_(1)` From `D` that of `A` is
`= sqrt(d^(2) + ((lambda)/(2))^(2)) - d(d - lambda//2) = d (1 + (lambda^(2))/(4 d^(2)))^(1//2) - d + (lambda)/(2) = d(1 + (lambda^(2))/(8 d^(2))) - d + (lambda)/(2) ~= (lambda)/(2)` (`because d gt gt lambda`)
Therefore, phase diff. is `pi`
`y_(D) = a cos (omega t - pi) = - a cos omega t`
Hence the signal picked up at `R_(1)` from all the four sources is
`y_(R_(1)) = y_(A) + y_(B) + y_(C) + y_(D) = a cos omega t - a cos omega t + a cos omega t - a cos omega t = 0`. ...(i)
Let the the signal picked up at `R_(2)` from to be `y_(B) = a_(1) cos omega t`
Path differecne of signals at `R_(2)` from `D` to that from `B` is `lambda//2`. Therefore, `y_(D) = a_(1) cos (omega t - pi)`
`= - a_(1) cos omega t`.
Again, path diff. of signals at `R_(2)` from `B` and `A` is
`= sqrt(d^(2) + (lambda//2)^(2)) - d = d (1 + (lambda^(2))/(4 d^(2)))^(1//2) -d = (1)/(8)(lambda^(2))/(d^(2))`
As `d gt gt lambda`, therefore this path diff. `rarr 0`, and phase diff. `phi rarr 0 :. y_(A) = a_(1) cos (omega t - phi)`
Similarly, `y_(C) = a_(1) cos (omega t - phi)`
Hence the signal picked up at `R_(2)` from all the four sources is
`y_(R_(2)) = y_(A) + y_(B) + y_(C) + y_(D) = a_(1) cos (omega t - phi) + a_(1) cos omega t + a_(1) cos (omega t - phi) - a_(1) cos omega t`
`y_(R_(2)) = 2 a_(1) cos (omega t - phi)` ...(ii)
Hence receiver `R_(2)` picks up the larger signal.
(ii) If source `B` is swithched off, then from (i),
`y_(R_(1)) = a cos omega t lt I_(R_(1)) gt = a^(2) lt cos^(2) omega t gt = (a^(2))/(2)`
From (ii), `y_(R_(2)) = a_(1) cos (omega t - phi) = a_(1) cos omega t, because phi rarr 0 lt I_(R_(2)) gt = a_(1)^(2) lt cos^(2) omega t gt = (a_(1)^(2))/(2) = (a^(2))/(2)`.
Hence `R_(1)` and `R_(2)` pick up the same signal.
(iii) When source `D` is swithched off, `Y_(R_(1)) = a cos omega t`
`:. lt I_(R_(1)) gt = (a^(2))/(2)` and `y_(R_(2)) = 3a cos omega t` (Taking `phi rarr 0`)
`lt I_(R_(2)) gt = 9 a^(2) lt cos^(2) omega t gt = (9)/(2)a^(2)` `:. R_(2)` picks up larger signal compared to `R_(1)`.
(iv) Hence a signal at `R_(1)` indicates that source `B` has been switched off and an anhanced signal at `R_(2)` indicates that source `D` has been switched off.

Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Four identical monochromatic sources A,B,C,D as shown in the (figure) produce waves of the same wavelength lambda and are coherent. Two receiver R_(1) and R_(2) are at great but equal distances from B. (i) Which of the two receivers picks up the larger signal when B is turned off? (iii) Which of the two receivers picks up the larger singnal when D is turned off ? (iv) Which of the two receivers can distinguish which of the sources B or D has been turned off ?
Four identical coherent sourc e emiting monochromatic light if same wavelength lambda are placed at A,B,C and D as shown. Two receivers R_(1) and R_(2) are at but equal distance from B. The path difference between signals reaching from A&D at R_(1) is (lambda)/(2) and between signals reaching from A & B at R_(2) is ~= 0 . Also assume that intensities of waves emitted by A,B,C &D reaching at R_(1) and R_(2) is same.
Two coherent point sources S_1 and S_2 are separated by a small distance d as shown. The fringes obtained on the screen will be
Some energy levels of a molecule are shown in the figure. The ratio of the wavelengths r = lambda_1//lambda_2 is given by -
Four identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
Four cars A, B and C are moving on a levelled road. Their distance versus time graphs are shown in Fig. Choose the correct statement
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance sqrt(2) d from the source and the detector as shown in figure. The source emits a wave of wavelength = d//2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?