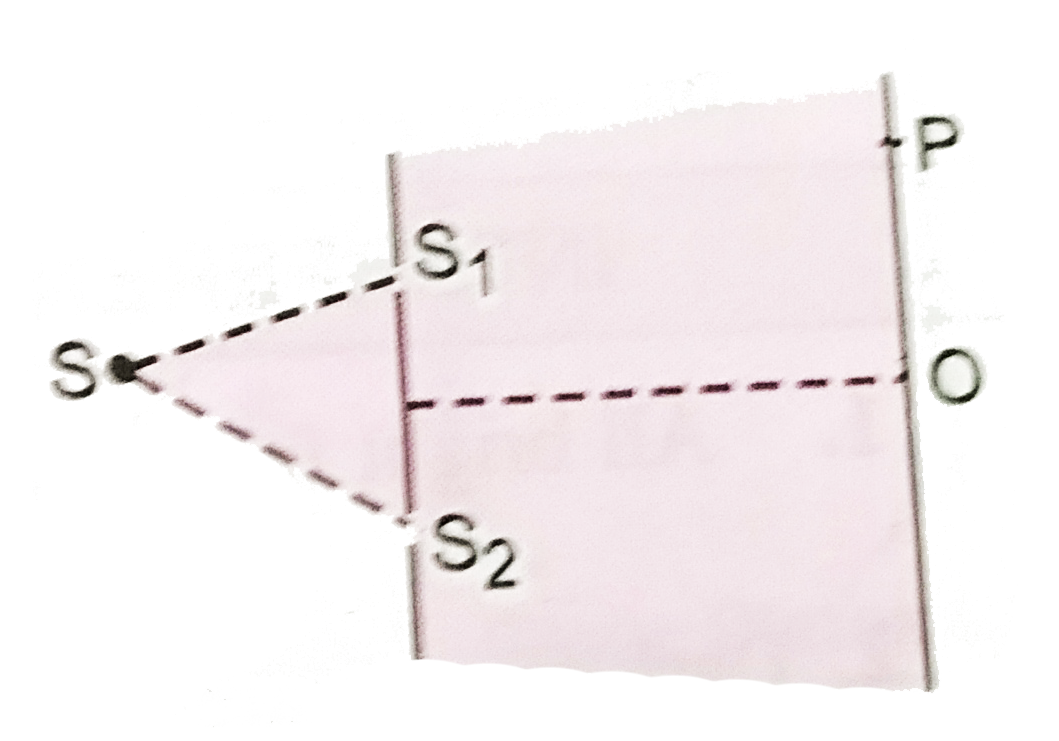
Fig. shows an experimental set up simillar to Young's double slit experiment to observe interference of light. Here `SS_(2) - SS_(1) = lambda//4`. Write down the conditions of (i) Contstructive interference
(ii) Destructive interference at any point `P` in terms of path diff. `(S_(2)P - S_(1)P)`. Does the central fringe observed in the above set up lie above or below `O` ? Give reason.

Explanation

Here, initial path diff. `SS_(2) - SS_(1) = lambda//4`.
`:.` For construcitve interference, net path diff. `S_(2)P - S_(1)P = (n lambda - lambda//4) = (n - (1)/(4)) lambda` …(i)
and for destructive interference, net path diff. `S_(2)P - S_(1)P = (n + (1)/(2))lambda - (lambda)/(4) = (n + (1)/(4))lambda`
For central maximum, `n = 0` `:.` From (i), path diff. `= - lambda//4`
The minus sign shows that cebtral maximum appears below `O`, at a distance `= lambda//4`.